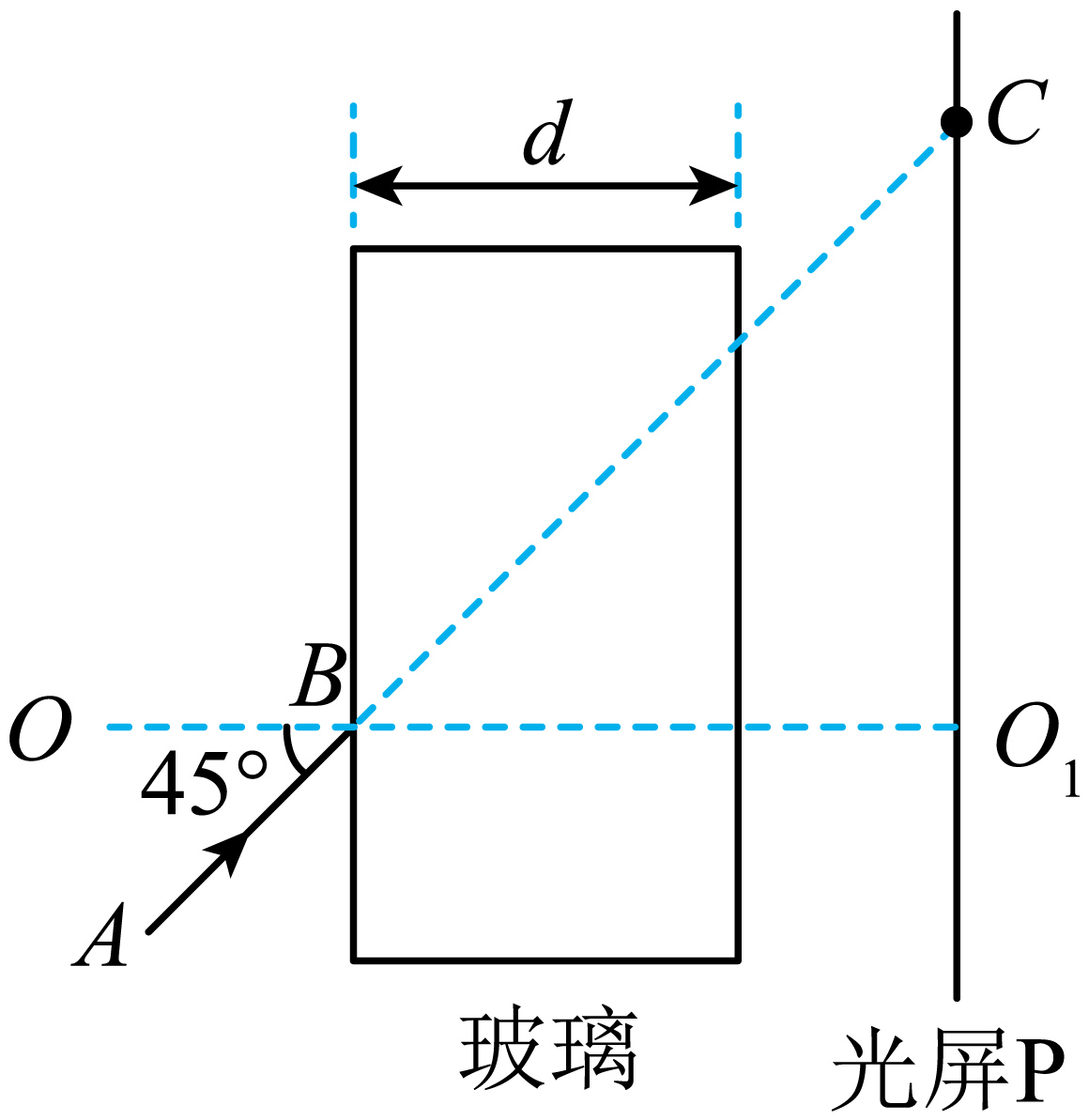
该玻璃的折射率；

$\\dfrac{\\sqrt{10}}{2}$；

光通过玻璃砖折射后出射光线与入射光线平行，过$D$点作$DM // CN$，完成光路图如图所示

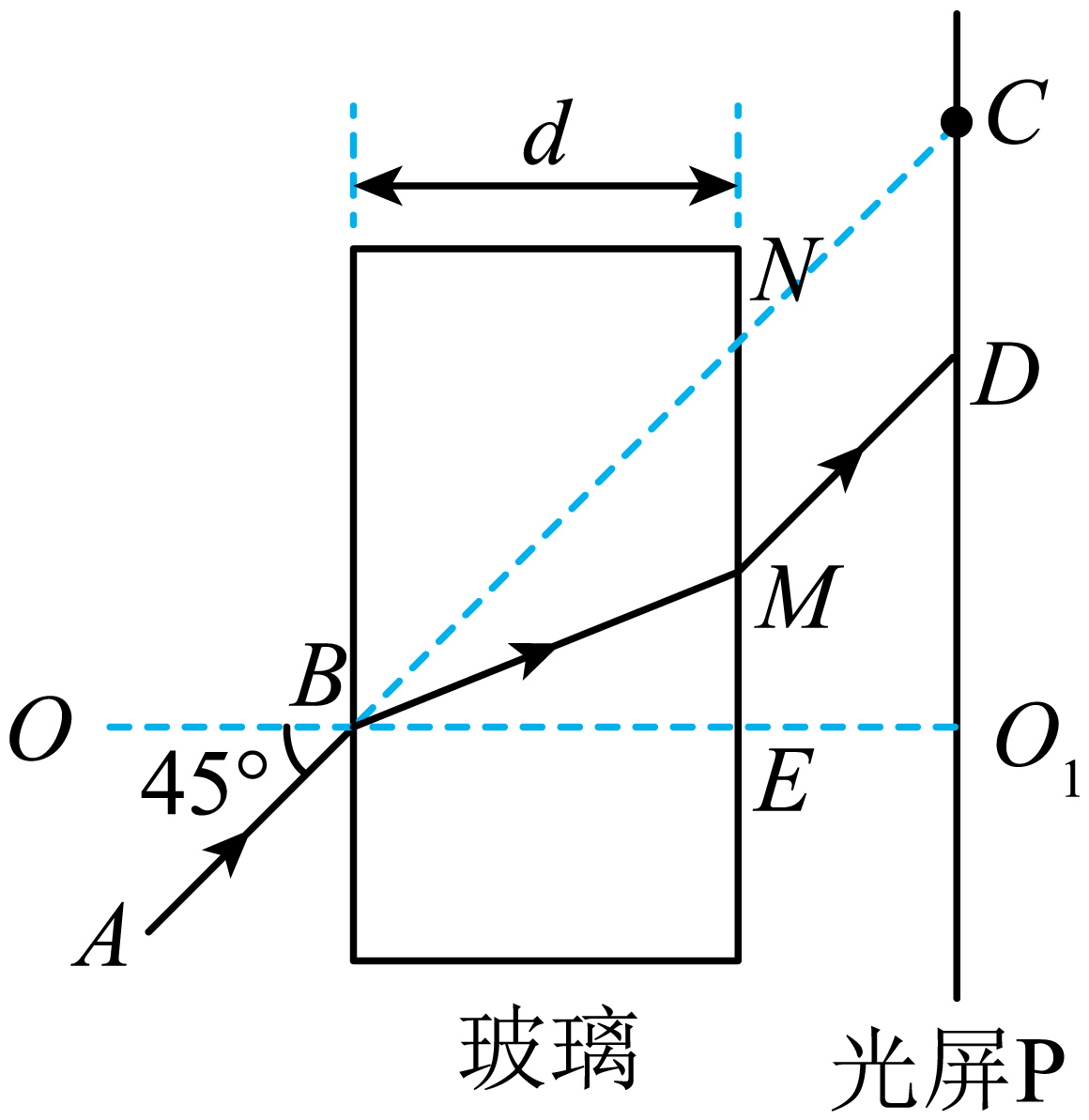
由几何关系可得$NE=BE=d$，$ME=NE-MN=NE-CD=\dfrac{d}{2}$，$BM=\sqrt{BE^{2}+ME^{2}}=\dfrac{\sqrt{5}}{2}d$

所以$\sin\angle MBE=\dfrac{ME}{BM}=\dfrac{1}{\sqrt{5}}$

根据折射定律可得$n=\dfrac{\sin\angle ABO}{\sin\angle MBE}=\dfrac{\sqrt{10}}{2}$；

由于放入平板玻璃，光到达光屏的时间改变了多少？

$\\dfrac{\\sqrt{2}d}{4c}$。

没有玻璃时，从左界面到右界面所需时间为$t_{1}=\dfrac{BN}{c}= \dfrac{\sqrt{2}d}{c}$

放上玻璃时，从左界面到右界面所需时间为$t_{2}=\dfrac{BM}{v}$，$v=\dfrac{c}{n}=\dfrac{\sqrt{10}}{5}c$

解得$t_{2}=\dfrac{5\sqrt{2}d}{4c}$

所以$\Delta t=t_{2}-t_{1}=\dfrac{\sqrt{2}d}{4c}$。