| 斜面问题 题目答案及解析
稿件来源:高途
| 斜面问题题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.6 用牛顿运动定律解决问题(一)
斜面问题
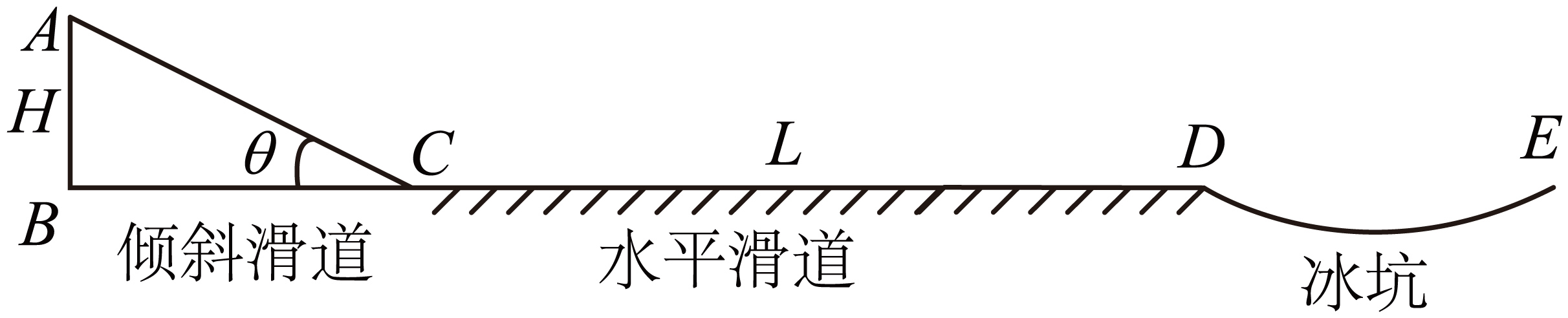
如图所示,某游乐场雪滑梯是由倾斜滑道、水平滑道平滑连接组成。已知倾斜滑道高度$H=11\;\rm m$,它与水平地面夹角$\theta=25^\circ $,水平滑道长度为$L$,滑道全程动摩擦因数$\mu =0.2$。水平滑道末端有一光滑球面冰坑,冰坑$DE$两点高度相同,冰坑的球面半径$R=90\;\rm m$($R$远大于弧长$DE$)。$g=10\;\rm m/s^{2}$,$\sin25^\circ =0.4$,$\cos25^\circ =0.9$。游客从雪滑梯顶部由静止下滑。
若游客在冰坑前停下,则水平滑道长度$L$是多少?
$30.25\\;\\rm m$;
"]]由已知题意可知,游客在$AC$间做匀加速直线运动,在$CD$间做匀减速直线运动,若游客在$D$点速度为零,由动能定理可得$mgH-\mu mg\cos 25^\circ \cdot \dfrac{H}{\sin 25^\circ}-\mu mgL=0$
解得$L=30.25\;\rm m$;
若游客以很小的初速度滑下,刚好能进入冰坑到达$E$点,求该游客从开始下滑到$E$点全程所用时间。(初速度可忽略,结果可以保留$\pi$)
$(10.5+3\\pi)\\;\\rm s$
"]]因游客以很小速度开始下滑,因此可看成初速度为$0$。设游客在倾斜滑道的加速度为$a_{1}$,滑行时间为$t_{1}$,到达$C$点时速度为$vC$,在水平滑道的加速度为$a_{2}$,滑行时间为$t_{2}$,根据牛顿第二定律可得$mg\sin 25^\circ − \mu mg\cos 25^\circ =ma_{1}$
解得$a_{1}=2.2\;\rm m/s^{2}$
由$x=\dfrac{1}{2}a_{1}t_{1}^{2}$
解得$t_{1}=5$
根据速度$—$时间公式可知$v_{C}=a_{1}t_{1}=11\;\rm m/s$
同理,根据牛顿第二定律可得$\mu mg=ma_{2}$
解得$a_{2}=2\;\rm m/s^{2}$
根据速度$—$时间公式有$v_{C}=a_{2}t_{2}$
解得$t_{2}=5.5\;\rm s$
因为冰坑为光滑球面,且半径远大于弧长,则游客在冰坑中的运动可看成等效单摆,由单摆周期公式$T=2\pi\sqrt{\dfrac{R}{g}}$
解得$t_{3}=\dfrac{1}{2}T=3\pi\;\rm (s)$
综上所述$t=t_{1}+t_{2}+t_{3}=(10.5+3\pi)\;\rm s$。
| 斜面问题题目答案及解析(完整版)
