高中 | 带电粒子在匀强电场中的偏转运动 题目答案及解析
稿件来源:高途
高中 | 带电粒子在匀强电场中的偏转运动题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
带电粒子在匀强电场中的偏转运动
如图所示,在直角坐标系xOy中,第一象限有竖直向上的匀强电场,第二、四象限有垂直纸面向里的匀强磁场。已知质量为m、电荷量为-q的粒子从x轴上的M点以速度v0沿y轴正方向进入第二象限,经y轴上N点沿x轴正方向射入第一象限,再从x轴上P点进入第四象限,经y轴上的Q点(图中未画出)射出磁场。已知第二、四象限匀强磁场的磁感应强度大小均为$B=\frac{mv_{0}}{qd}$(d为已知量),粒子在P点的速度与x轴正方向成45°角,不计粒子的重力。求:
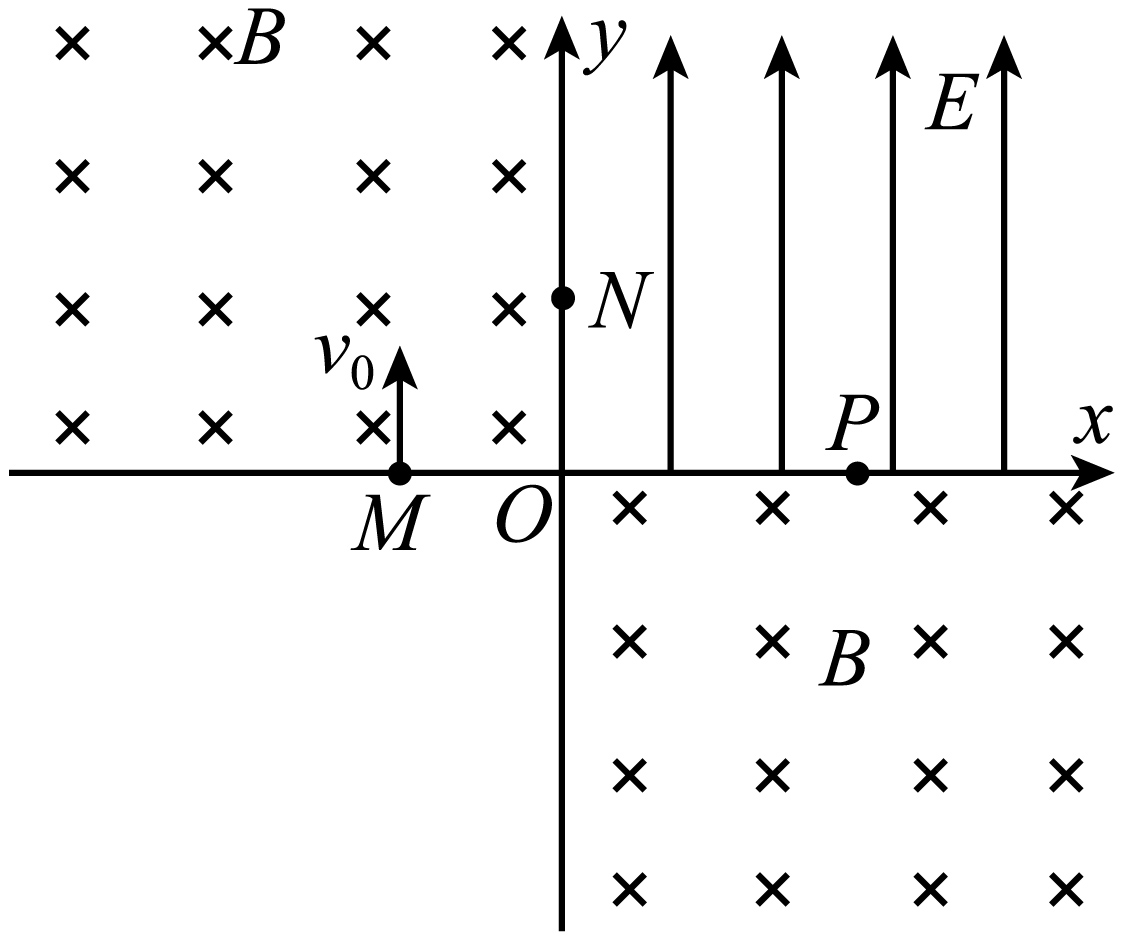
ON的长度;
d
"]]粒子的运动轨迹如图所示
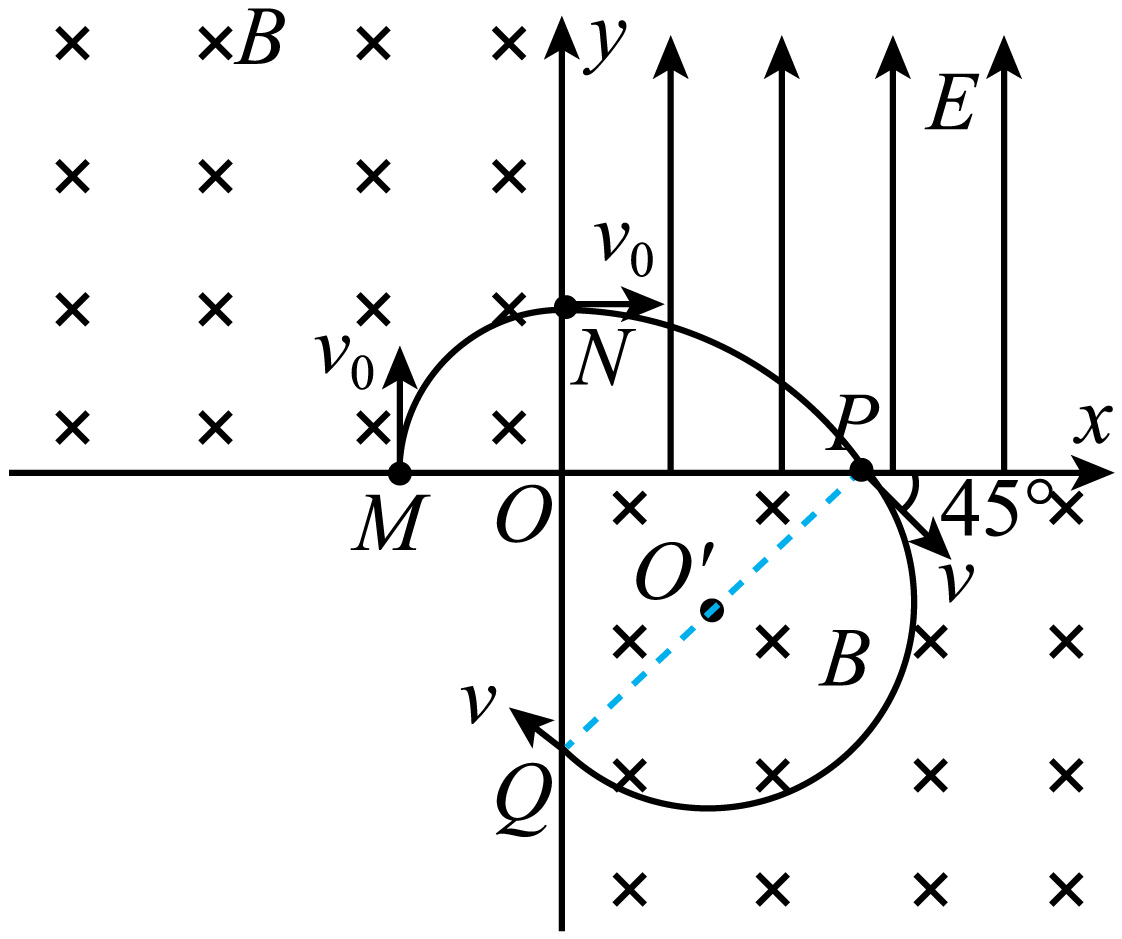
设粒子在磁场中的轨迹半径为r,则$qBv_{0}=\frac{mv_{0}^{2}}{r}$
解得$r=d$
所以$ON=r=d$
匀强电场的场强大小和OP的长度;
$\\frac{mv_{0}^{2}}{2qd}$,2d
"]]粒子进入电场中做类平抛运动,则$qE=ma$,$d=\frac{1}{2}at^{2}$,$\tan 45{^\circ}=\frac{at}{v_{0}}$
联立以上各式解得$E=\frac{mv_{0}^{2}}{2qd}$
水平方向有$OP=v_{0}t$
联立以上各式解得$OP=2d$
PQ的长度。
$2\\sqrt{2}d$
"]]根据几何关系有$\cos 45{^\circ}= \frac{v_{0}}{v}$
所以$v=\sqrt{2}v_{0}$
又$qBv=\frac{mv^{2}}{R}$
联立以上各式可得$R=\sqrt{2}d$
所以$PQ=2R=2\sqrt{2}d$
高中 | 带电粒子在匀强电场中的偏转运动题目答案及解析(完整版)
