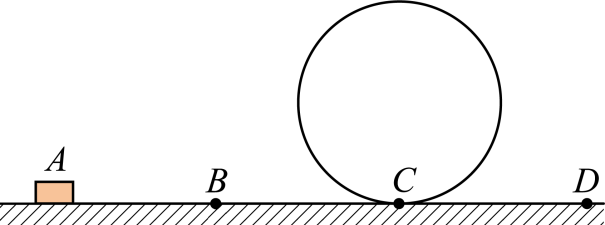
当滑块再回到圆轨道最低点时圆轨道对它的弹力大小；

$120\\;\\rm N$；

滑块恰好通过最高点，滑块只受到重力，此时重力提供向心力，根据牛顿第二定律可得$mg=m\dfrac{v^{2}}{R}$

滑块从$C$点到最高点过程由动能定理可得$- mg \times 2R=\dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{C}^{2}$

在$C$点，对滑块由牛顿第二定律可知$F_{{N}}-mg=m\dfrac{v_{C}^{2}}{R}$

解得$v_{C}=10\;\rm m/s$

$F_{N}=120\;\rm N$；

滑块沿着出口的平直轨道$CD$能滑行的最大距离；

$10\\;\\rm m$；

平直轨道$CD$上滑行时，由动能定理可得$\dfrac{1}{2}mv_{C}^{2}=\mu mgx$

解得滑行距离$x=10\;\rm m$；

平直轨道$BC$段的长度。

$15\\;\\rm m$。

对$AC$过程由动能定理可得$FL-\mu mg\left( x_{BC}+L \right)=\dfrac{1}{2}mv_{C}^{2}$

解得$BC$长度$x_{BC}=15\;\rm m$。