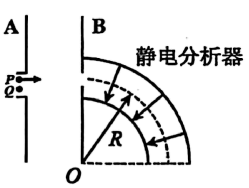
如图所示，$A$、$B$两平行板间距为$d$，$B$板与形状为四分之一圆弧的静电分析器左端重合，$A$、$B$两板间存在水平向右的匀强电场，静电分析器中存在沿半径方向指向圆心$O$的辐向电场。极板$A$上小孔的$P$点处有一质量为$m$、电荷量为$q$的带电粒子$X$，自$A$板由静止开始向右加速运动，并从极板$B$的小孔沿水平方向进入静电分析器，粒子在静电分析器中恰好沿图示虚线做匀速圆周运动。已知粒子做圆周运动的半径为$R$，轨迹处电场强度的大小均为$E$，粒子重力不计。下列说法正确的是$(\qquad)$

$A$、$B$极板间的电压为$U_{AB}=ER$

粒子从$P$点出发至离开静电分析器运动的总时间$t_{总}=(4d+\\pi R)\\sqrt{\\left( \\dfrac{m}{qER} \\right)}$

若粒子从$P$点正下方的$Q$点进入，在静电分析器中做匀速圆周运动的半径为$R'$，则轨迹处的场强$E'=\\dfrac{ER}{R'}$

若将$X$粒子更换为比荷为其两倍的$Y$粒子，要使$Y$粒子仍沿图中虚线做匀速圆周运动，需要将虚线处场强大小调整为$\\sqrt{2}E$

$\rm A$．带电粒子在静电分析器中恰好做匀速圆周运动，由电场力提供向心力，则有$Eq=\dfrac{mv^{2}}{R}$

解得$v=\sqrt{\dfrac{EqR}{m}}$，带电粒子在两平行板间加速，由动能定理可得$\dfrac{1}{2}mv^{2}=\dfrac{U_{\text{AB}}}{d}q \times d$，解得$U_{\text{AB}}=\dfrac{ER}{2}$，故$\rm A$错误；

$\rm B$．粒子从$P$点出发至离开静电分析器运动的总时间为$t=\dfrac{v-0}{\dfrac{E_{\text{AB}}q}{m}}+\dfrac{2\pi R \times \dfrac{1}{4}}{v}=\left( 2d+\dfrac{\pi R}{2} \right)\sqrt{\dfrac{m}{qER}}$，故$\rm B$错误；

$\rm C$．若粒子从$P$点正下方的$Q$点进入，在静电分析器中做匀速圆周运动的半径为$R^\prime$，则有$v=\sqrt{\dfrac{E'qR'}{m}}=\sqrt{\dfrac{EqR}{m}}$，变化可得$E'=\dfrac{ER}{R^{'}}$，故$\rm C$正确；

$\rm D$．根据动能定理可得$Y$粒子在两平行板间加速满足$\dfrac{1}{2}m_{\text{Y}}v_{\text{Y}}^{2}=\dfrac{U_{\text{AB}}}{d}q_{\text{Y}} \times d=\dfrac{ERq_{\text{Y}}}{2}$，解得$v_{\text{Y}}=\sqrt{\dfrac{ERq_{\text{Y}}}{m_{\text{Y}}}}$，$Y$粒子仍沿图中虚线做匀速圆周运动，则有$E'q_{\text{Y}}=\dfrac{m_{\text{Y}}v_{\text{Y}}^{2}}{R}$，解得$E'=E$，故$\rm D$错误。

故选：$\rm C$。