高中 | 运动的合成与分解 题目答案及解析
稿件来源:高途
高中 | 运动的合成与分解题目答案及解析如下,仅供参考!
必修2
第五章 曲线运动
5.1 曲线运动
运动的合成与分解
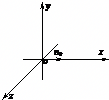
如图$ox$、$oy$、$oz$为相互垂直的坐标轴,$oy$轴为竖直方向,整个空间存在竖直向下的匀强磁场,磁感应强度大小为$B$,现有一质量为$m$、电量为$+q$的小球从坐标原点$O$以速度$\upsilon_{0}$沿$ox$轴正方向抛出(不计空气阻力,重力加速度为$g$)。求:
若在整个空间加一匀强电场$E_{1}$,使小球在$xoz$平面内做匀速圆周运动,求匀强电场的电场强度$E_{1}$和小球做匀速圆周运动的轨道半径$r$;
$E_{1}= \\dfrac{mg}{q}$,方向沿$y$轴正向,$\\ r= \\dfrac{mv_{0}}{qB}$;
"]]因为要小球在磁场中做匀速圆周运动,必须满足$qE_{1}=mg$
解得:$E_{1}=\dfrac{mg}{q}$,方向沿$y$轴正向
小球运动的过程中洛伦兹力提供向心力,得:$qvB=m\dfrac{v_{0}^{2}}{r}$
解得:$r=\dfrac{mv_{0}}{qB}$
若撤去磁场,在整个空间加一沿$y$轴正方向的匀强电场,电场强度为$E_{2}$$= \dfrac{3mg}{q}$,若仍将小球从坐标原点$O$以速度$\upsilon_{0}$沿$ox$轴正方向抛出,求该小球从坐标原点$O$抛出经过时间$t$后的动能$E_{k}$。
$E_{k}=\\dfrac{1}{2}m{v_{0}}^{2}+ 2mg^{2}t^{2}$
"]]小球在复合场中做类平抛运动,在 $y$轴方向上做初速为零的匀加速运动。
加速度为:$a=\dfrac{qE_{2}-mg}{m}=2g$
$y$轴方向的位移为:$y=\dfrac{1}{2}at^{2}$
由动能定理得:$(qE_{2}-mg)y=E_{k}-\dfrac{1}{2}m{v_{0}}^{2}$
解得:$E_{k}=\dfrac{1}{2}m{v_{0}}^{2}+2mg^{2}t^{2}$
高中 | 运动的合成与分解题目答案及解析(完整版)
