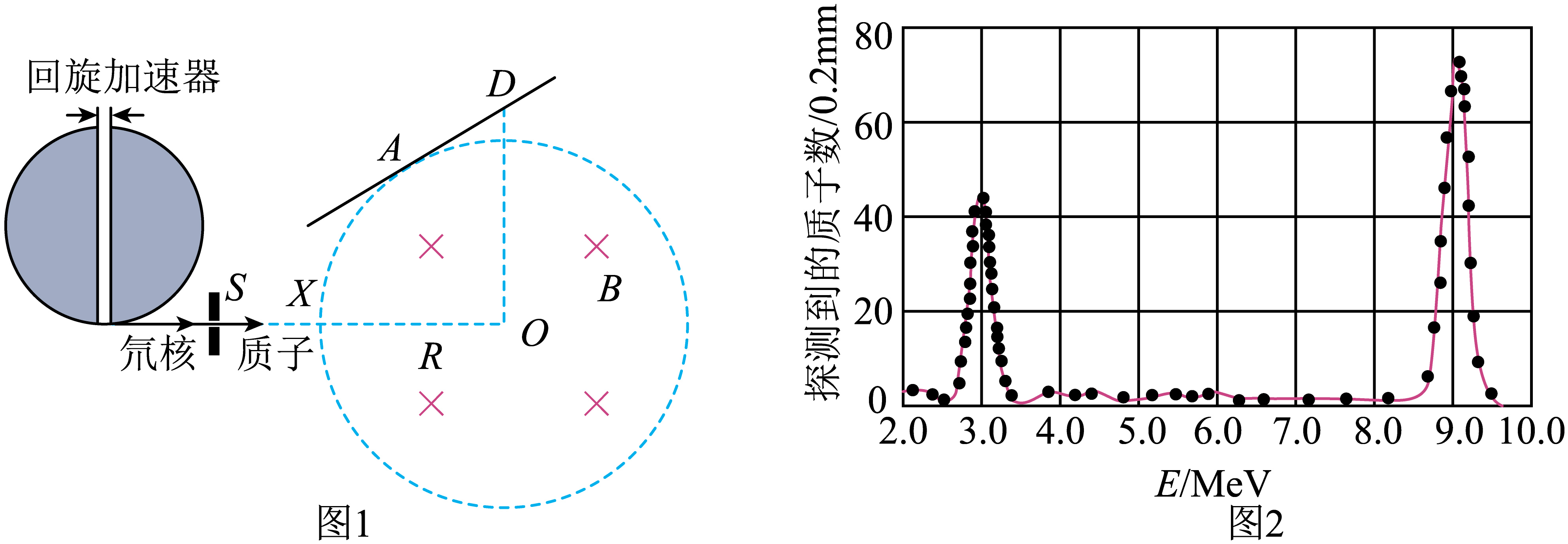
写出氘核撞击铝核的核反应方程；

$\\rm _{1}^{2}H+_{13}^{27}Al→_{13}^{28}Al+_{1}^{1}H$

氘核撞击铝核的核反应方程$\rm _{1}^{2}H+_{13}^{27}Al→_{13}^{28}Al+_{1}^{1}H$

求$A$、$D$的间距$L$；

$\\dfrac{\\sqrt{3}R}{3}$

由图可知，两种质子的动能分别为$3\;\rm MeV$和$9\;\rm MeV$，动能之比$1:3$，可知速度之比$1:\sqrt{3}$，根据$evB=m\dfrac{v^{2}}{r}$

可知$r=\dfrac{mv}{eB}$

可知在磁场中的半径之比为$r_{1}:r_{2}=1:\sqrt{3}$

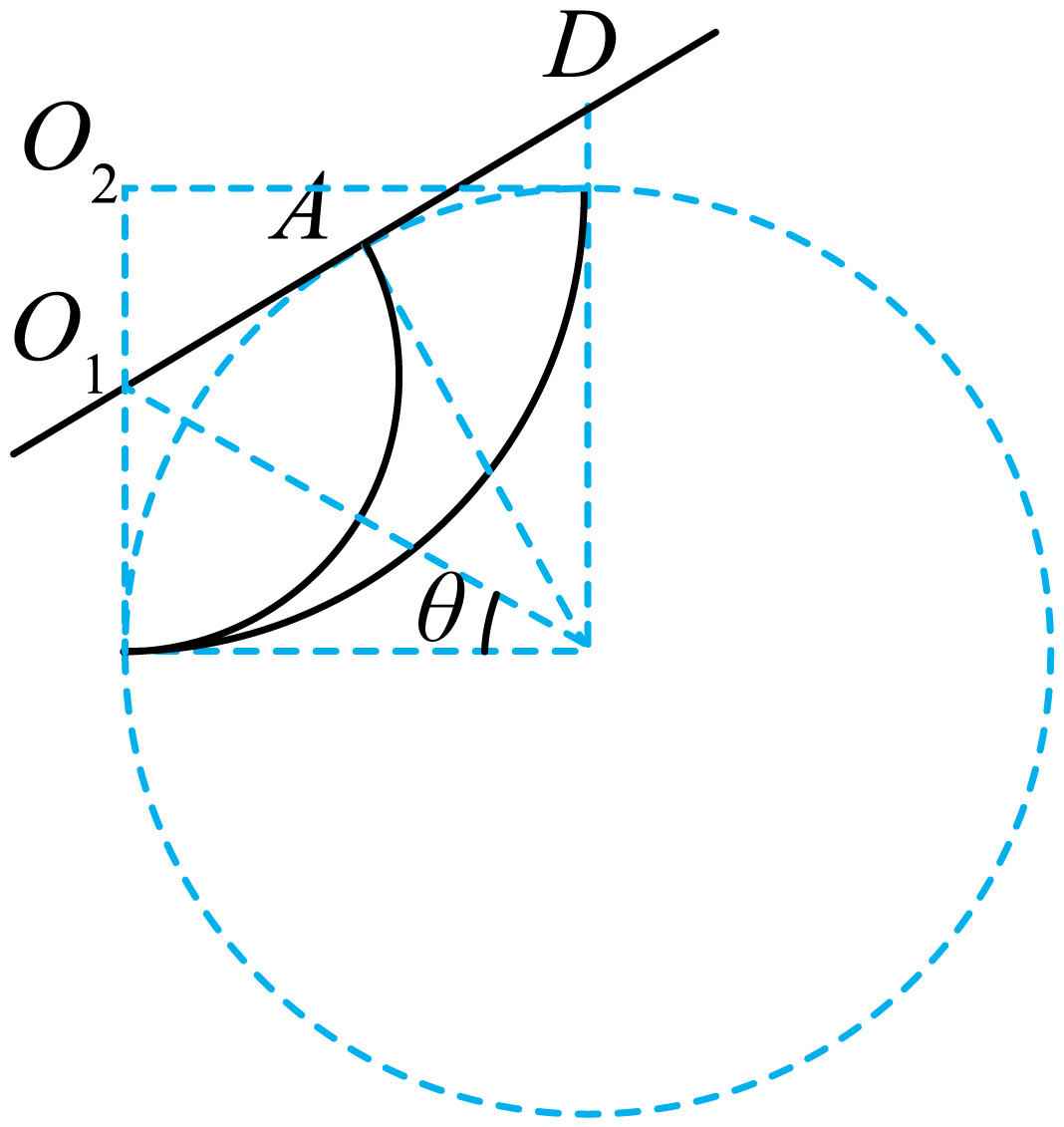
由图可知半径较小的打到$A$点，半径较大的打到$D$点，由几何关系可知$\dfrac{r_{1}}{R}=\tan\theta$，$r_{2}=R$

解得$\theta=30^\circ $

可得$A$、$D$的间距$L=R\tan 30{^\circ}=\dfrac{\sqrt{3}R}{3}$

若从回旋加速器引出的高能氘核流为$1.0\;\rm mA$，求回旋加速器的输出功率；

$2.74\\times 10^{3}\\;\\rm W$

若从回旋加速器引出的高能氘核流为$1.0\;\rm mA$，则时间$t$射出氘核的数量为$n=\dfrac{It}{e}$

回旋加速器的输出功率$P=\dfrac{nE}{t}=\dfrac{IE}{e}=\dfrac{10^{- 3}\;\rm \text{A} \times 2.74 \times 10^{6}\ \text{eV}}{e}=2.74 \times 10^{3}\;\rm \text{W}$

处于激发态的$\rm _{13}^{28}Al$核会发生$\beta$衰变，核反应方程是$\rm _{13}^{28}Al→_{14}^{28}Si+_{-1}^{0}e$。若$\rm _{13}^{28}Al$核质量等于$\rm _{14}^{28}Si$核质量，电子质量为$0.51\;\rm MeV/c^{2}$，在上述两个核反应过程中，原子核被视为静止，求衰变释放的能量。

$0.25\\;\\rm MeV$

反应之前氘原子核（$\rm _{1}^{2}H$）的动能为$2.74\;\rm MeV$，核反应产生处于某一激发态的同位素核（$\rm _{13}^{28}Al$）时生成的（$\rm _{1}^{1}H$）的动能为$3\;\rm MeV$；衰变释放能量$\Delta E=2.74\;{\rm MeV-3\;\rm MeV}+\Delta mc^{2}=0.25\;\rm MeV$。