| 静态平衡 题目答案及解析
稿件来源:高途
| 静态平衡题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.7 用牛顿运动定律解决问题(二)
静态平衡
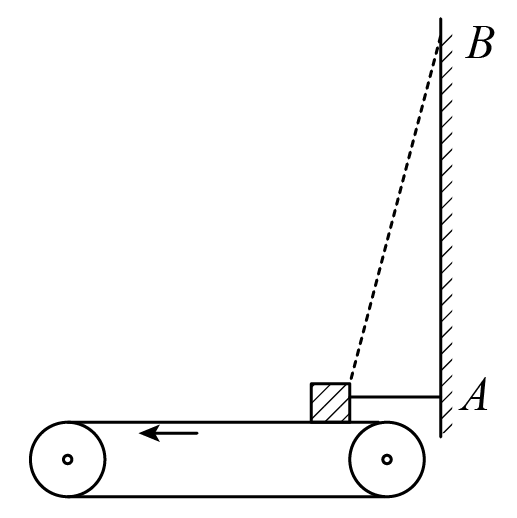
如图所示,水平传送带在电机带动下逆时针转动,开始时,质量为$m=1\;\rm kg$的物块在水平细绳$OA$的牵引下静止在传送带上,现以$O$点为中心,逆时针旋转细绳,调整拉力的方向,发现当细绳沿$OB$方向时,拉力方向与水平方向夹角$\theta=74^\circ $,细绳所受的拉力与细绳水平时相等,已知重力加速度$g=10\;\rm m/s^{2}$,$\sin 37^\circ =0.6$,$\cos 37^\circ =0.8$,求:
物块与传送带之间的动摩擦因数$\mu $;
$0.75$;
"]]当细线沿$OA$方向时,由平衡条件可得$T_{1}=\mu mg$
当细线沿$OB$方向时,正交分解可得$T_{1}\cos 74^\circ =\mu N_{1}$
$T_{1}\sin 74^\circ +N_{1}=mg$
联立解得$\mu =0.75$
拉力的最小值及此时拉力与水平方向的夹角$\alpha$。
$6\\;\\rm N$,$37^\\circ$
"]]细绳与水平方向夹角为$\alpha$,由平衡条件可得$T\cos \alpha=\mu N$
$T\sin \alpha+N=mg$
联立可得$T=\dfrac{\mu mg}{\cos\alpha+\mu\sin\alpha}=\dfrac{\mu mg}{\sqrt{1+\mu^{2}}\sin(\beta+\alpha)}$
其中$\tan\beta=\dfrac{1}{\mu}$
当$\sin (\beta+\alpha)=1$
即$\alpha=37^\circ $
时,拉力最小,拉力最小值为$T_{\min}=\dfrac{\mu mg}{\sqrt{1+\mu^{2}}}=6\;\rm \text{N}$
| 静态平衡题目答案及解析(完整版)
