| 静态平衡 题目答案及解析
稿件来源:高途
| 静态平衡题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.7 用牛顿运动定律解决问题(二)
静态平衡
某探究小组利用橡皮筋完成下面实验。
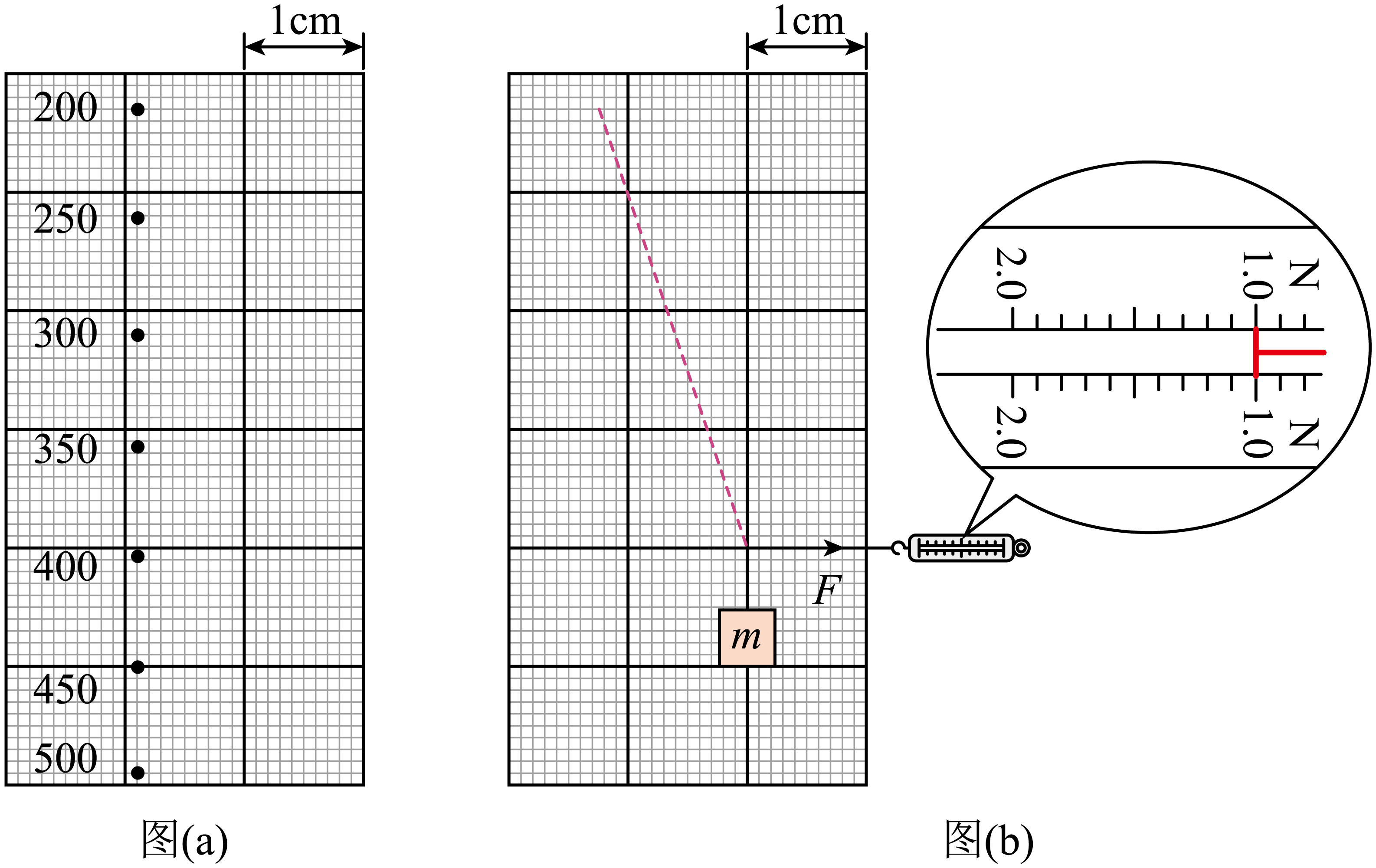
将粘贴有坐标纸的木板竖直放置。橡皮筋的一端用图钉固定在木板上,另一端悬挂钩码。钩码质量分别为$200\;\rm g$、$250\;\rm g$、⋯、$500\;\rm g$,平衡时橡皮筋底端在坐标纸上对应的位置如图($a$)中圆点所示(钩码的质量在图中用数字标出)。悬挂的钩码质量分别为$200\;\rm g$和$300\;\rm g$时,橡皮筋底端位置间的距离为 $\;\rm cm$;
根据图($a$)可知悬挂的钩码质量分别为$200\;\rm g$和$300\;\rm g$时,橡皮筋底端位置间的距离为$1.90\;\rm cm$;
根据图($a$)中各点的位置可知,在所测范围内橡皮筋长度的增加量与所挂钩码的 (选填“质量”或“质量的增加量”)成正比,由此可求出橡皮筋的劲度系数为 $\:\rm{{N}}/{{m}}$(保留$2$位有效数字,重力加速度取$9.8\;\rm m/s^{2}$);
根据图像可知钩码每增加相同的质量橡皮筋增加相同的长度,故在所测范围内橡皮筋长度的增加量与所挂钩码的质量的增加量成正比。
设橡皮筋原长为$L_{0}$,劲度系数为$k$,根据胡克定律$F=kx$;其中$F=mg$,$x$为橡皮筋长度的增加量。
设悬挂质量为$m_{1}$、$m_{2}$的钩码时,橡皮筋长度的增加量分别为$x_{1}$、$x_{2}$,则$m_{1}g=kx_{1}$,$m_{2}g=kx_{2}$
两式相减得$(m_{2} − m_{1})g=k(x_{2} − x_{1})$
取$m_{1}=200g=0.2\;\rm kg$,$m_{2}=300g=0.3\;\rm kg$,$\Delta x=x_{2} − x_{1}=1.9\;\rm cm=1.9 \times 10^{-2}\;\rm m$
根据$(m_{2} − m_{1})g=k(x_{2} − x_{1})$,可得$k=\dfrac{\left( m_{2}-m_{1} \right)g}{x_{2}-x_{1}}=\dfrac{(0.3-0.2) \times 9.8}{1.9 \times 10^{- 2}}\;\rm {N/m} \approx {52\;\rm N/m}$;
悬挂的钩码质量为$m$时,在橡皮筋底端施以水平向右的力$F$,平衡时橡皮筋方向如图($b$)中虚线所示,图($b$)中测力计的示数给出了力$F$的大小,则$F=$ $\;\rm N$,$m=$ $\;\rm g$(选填“$200$”“$300$”或“$400$”)。
根据图($b$)可知$F=1.00\;\rm N$;设橡皮筋与竖直方向夹角为$\theta$,对橡皮筋下端点进行受力分析有$\tan\theta=\dfrac{F}{mg}$;从图中可知$\tan\theta \approx \dfrac{12}{37}$,结合$F=1.0\;\rm N$
可得$m ≈ 0.31\;\rm kg$,所以取$m=300\;\rm g$。
| 静态平衡题目答案及解析(完整版)
