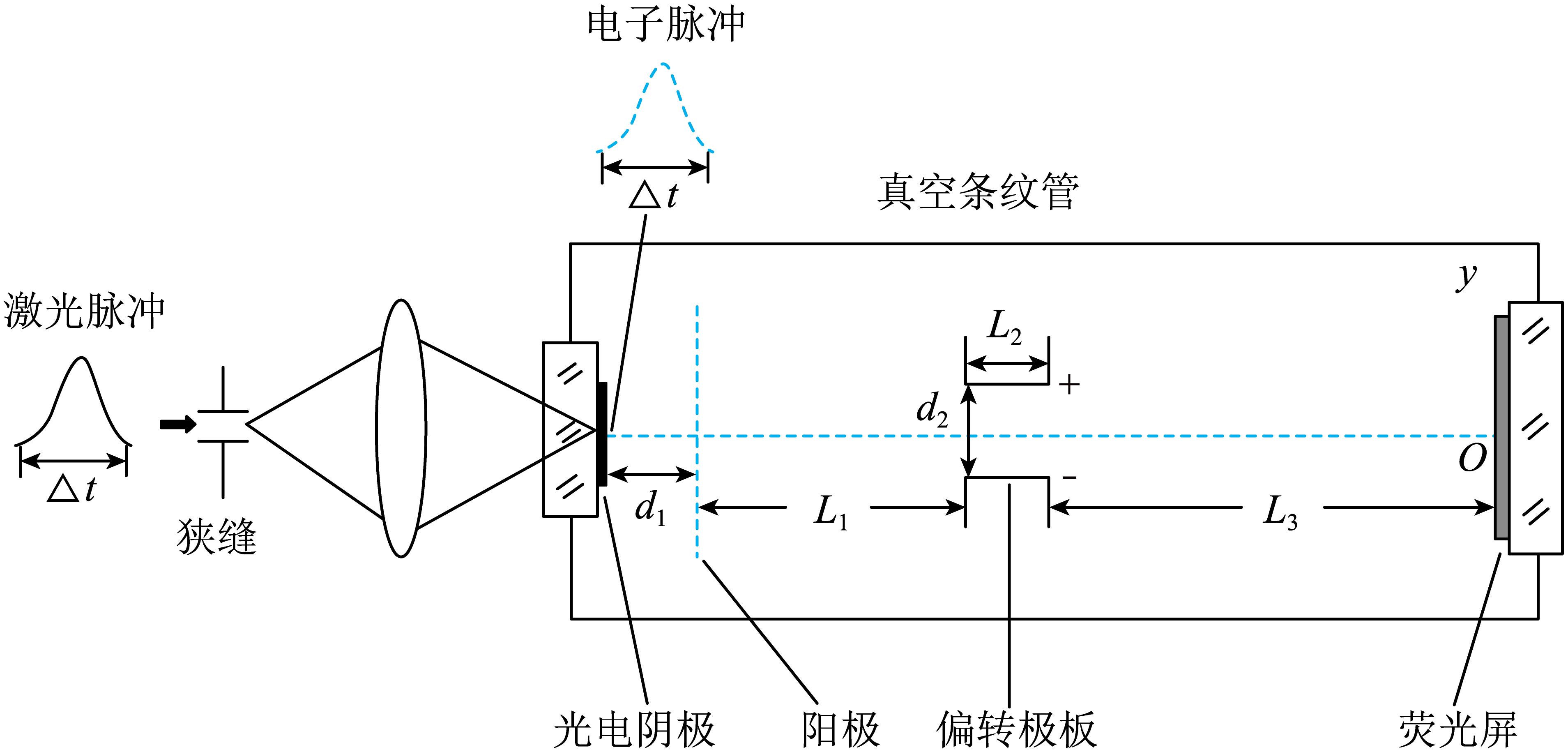
现有多碱、$Au$和$CsI$三种常用的光电阴极材料，它们的逸出功分别约为$1.1\;\rm eV、4.5\;\rm eV、6.2\;\rm eV$。若要使波长范围为$200 ∼ 900\;\rm nm$的入射激光都能打出光电子，请通过定量分析确定应选用哪种光电阴极材料。$(1\;\rm eV=1.6 \times 10^{-19}\;\rm J)$

多碱

根据题意，设入射激光波长为$\lambda$，则对应的光子能量为$\varepsilon=h\nu=\dfrac{hc}{\lambda}$

可得波长范围为$200 ∼ 900\;\rm nm$的入射激光的能量范围为$1.38\;\rm eV ∼ 6.2\;\rm eV$

要使入射激光都能打出光电子，则所有入射激光的能量应大于光电阴极材料的逸出功，所以应选择多碱光电阴极材料。

当偏转极板间电压$U$为常数时，求电子打在荧光屏上的位置。

$\\dfrac{UL_{2}\\left( L_{2}+2L_{3} \\right)}{4U_{1}d_{2}}$

电子在光电阴极与阳极之间做匀加速直线运动，设电子在此过程中的加速度大小为$a_{1}$，运动时间为$t_{1}$，离开阳极时的速度大小为$v_{1}$，则有$a_{1}=\dfrac{eU_{1}}{md_{1}}$，$v_{1}^{2}=2a_{1}d_{1}$，$d_{1}=\dfrac{1}{2}a_{1}t_{1}^{2}$

电子在离开阳极到偏转极板左端的过程中做匀速直线运动，设运动时间为$t_{2}$，则$L_{1}=v_{1}t_{2}$

当偏转电压$U$为常数时，电子在偏转极板内水平方向做匀速直线运动，在竖直$y$方向做匀加速直线运动。设$y$方向的加速度大小为$a_{2}$，在偏转极板内运动时间为$t_{3}$，离开偏转极板时$y$方向速度为$v_{y}$，偏转位移为$y_{1}$，则$a_{2}=\dfrac{eU}{md_{2}}$，$L_{2}=v_{1}t_{3}$，$v_{y}=a_{2}t_{3}$，$y_{1}=\dfrac{1}{2}a_{2}t_{3}^{2}$

设电子离开偏转极板至打到荧光屏上的时间为$t_{4}$，在此时间内电子在$y$方向的位移为$y_{2}$，则$L_{3}=v_{1}t_{4}$，$y_{2}=v_{y}t_{4}$

设电子离荧光屏中心的距离为$y$，则$y=y_{1}+y_{2}$

联立解得$y=\dfrac{UL_{2}\left( L_{2}+2L_{3} \right)}{4U_{1}d_{2}}$

真实情况下，偏转极板间电压$U$与时间$t$的关系为$U=U_{0}+kt$（$U_{0}$和$k$为大于零的常数），其零时刻与激光脉冲刚入射至光电阴极的时刻相同。

①求最后进入偏转极板间的电子离开偏转极板时$y$方向速度的大小：

②若$L_{2}$小且$L_{2} ≪ L_{3}$，此时可忽略不同时刻电子在偏转极板间$y$方向位移的差别，求电子脉冲在荧光屏上的空间宽度$\Delta y$与激光脉冲持续时间$\Delta t$的关系。

①$\\left( U_{0}+k\\Delta t \\right)\\dfrac{L_{2}}{d_{2}}\\sqrt{\\dfrac{e}{2mU_{1}}}+\\left( 4d_{1}+ 2L_{1}+L_{2} \\right)\\dfrac{kL_{2}}{4U_{1}d_{2}}$；②$\\Delta y=\\dfrac{kL_{2}L_{3}}{2U_{1}d_{2}}\\Delta t$

当偏转极板间电压$U=U_{0}+kt$时，电子在偏转极板内$y$方向做加速度线性增加的变加速直线运动。

①在$t_{1}+t_{2}+\Delta t$时刻，最后的电子进入偏转极板间，此时极板间的电压为$U_{0}+k(t_{1}+t_{2}+\Delta t)$，设电子在偏转极板内运动时$y$方向的加速度为$a_{3}$，离开偏转极板时$y$方向的速度为$v_{y2}$，则$a_{3}=\dfrac{e\left( U_{0}+kt \right)}{md_{2}}$

则$a_{3} − t$图像，如图所示

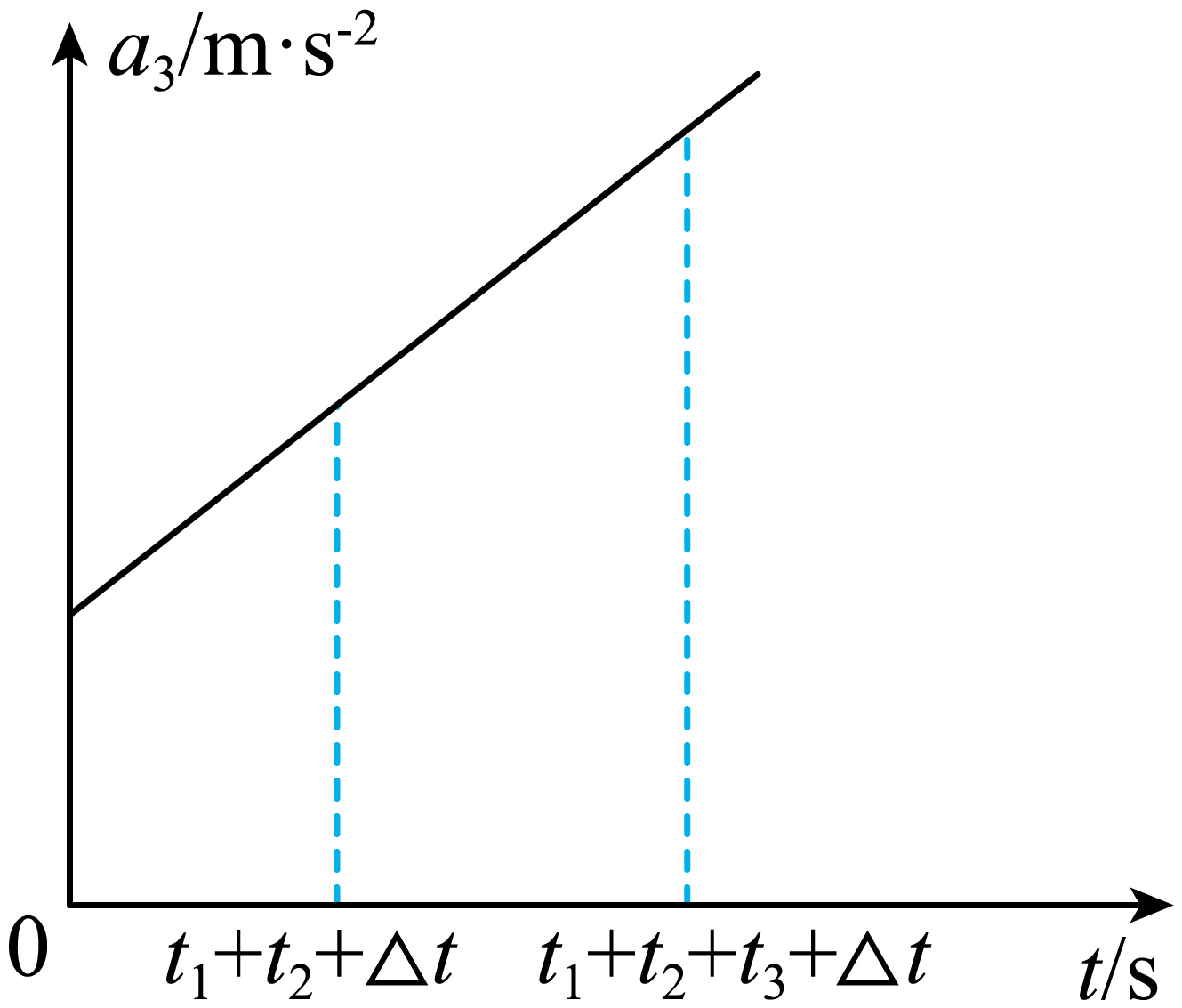
由上述分析，结合图像可得$v_{y2}=\left\lbrack U_{0}+k\left( t_{1}+t_{2}+\Delta t \right)+\dfrac{kt_{3}}{2} \right\rbrack\dfrac{et_{3}}{md_{2}}$

联立小问$2$分析可得$v_{y_{2}}=\left( U_{0}+k\Delta t \right)\dfrac{L_{2}}{d_{2}}\sqrt{\dfrac{e}{2mU_{1}}}+\left( 4d_{1}+2L_{1}+L_{2} \right)\dfrac{kL_{2}}{4U_{1}d_{2}}$

②在$t_{1}+t_{2}$时刻，最前面的电子进入偏转极板间，此时极板间的电压为$U_{0}+k(t_{1}+t_{2})$。同理可得，该电子离开偏转极板时$y$方向的速度$v_{y1}$，则有$v_{y1}=\left\lbrack U_{0}+k\left( t_{1}+t_{2} \right)+\dfrac{kt_{3}}{2} \right\rbrack\dfrac{et_{3}}{md_{2}}$

设电子脉冲打在荧光屏上的空间宽度为$\Delta y$，电子从离开偏转极板至打到荧光屏上的时间为$t_{4}$，则$L_{3}=v_{1}t_{4}$，$\Delta y=(v_{y2} − v_{y1})t_{4}$

联立解得$\Delta y=\dfrac{kL_{2}L_{3}}{2U_{1}d_{2}}\Delta t$