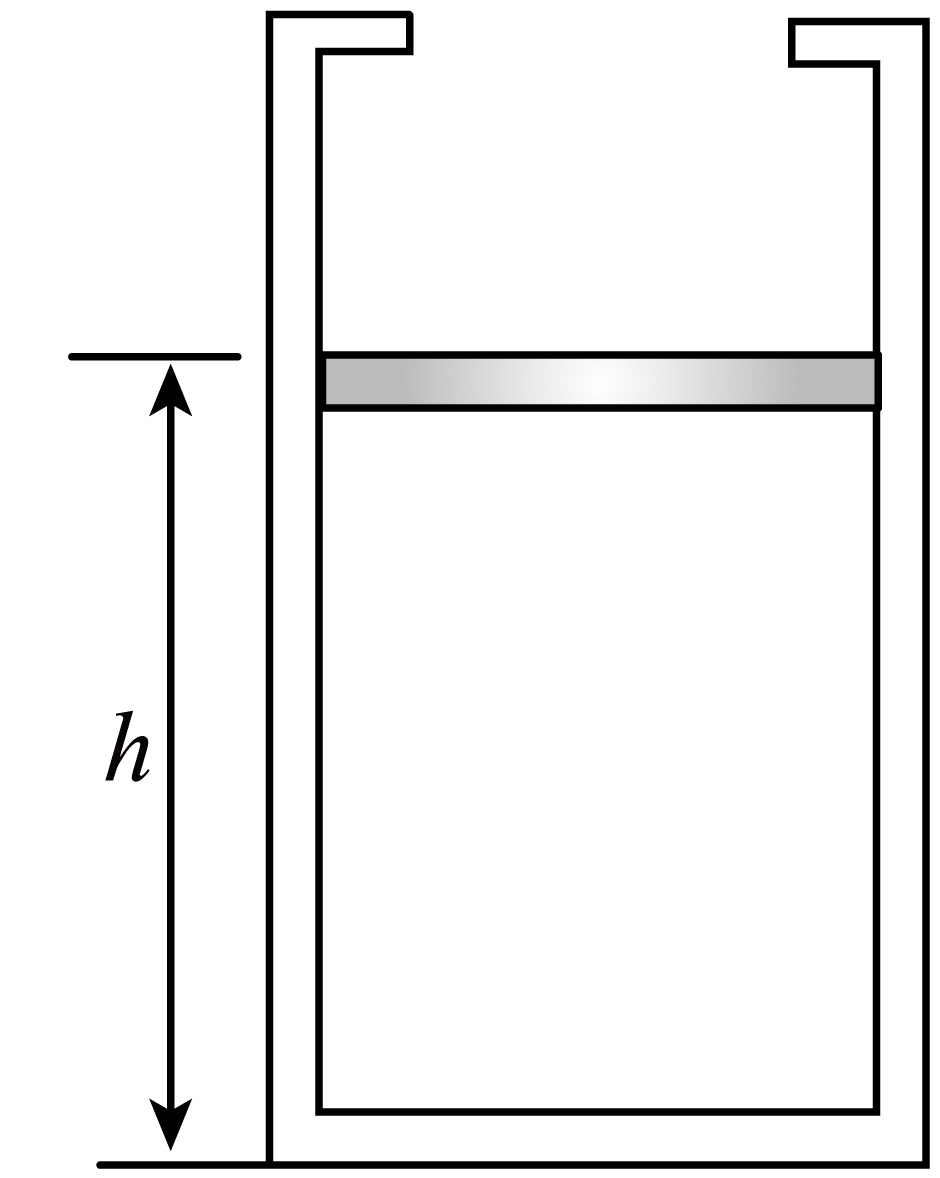
环境温度逐渐升高，活塞运动至卡口前的过程中，气体分子的平均动能                 （选填“增加”、“减少”或“不变”），气缸内壁单位面积受到的压力                 （选填“增大”、“减小”或“不变"）：

气体分子的平均动能随温度的变化而变化，由题知环境温度逐渐升高，且气缸的导热性能良好，故气体的温度也逐渐升高，所以气体分子的平均动能增加；

对活塞受力分析，根据平衡条件有$p_{1}S=p_{0}S+mg$

可知压强$p_{1}$是一个定值，即在活塞到达卡扣前气体做等压变化；

根据$F=p\Delta S$

可知圆筒内壁单位面积受到的压力不变。

活塞恰好到达容器卡口处时的环境温度；

$T_{2}=375\\;\\rm K$（或$t_{2}=102^\\circ\\rm C$）

在初始状态，对活塞受力分析，根据平衡条件有$p_{1}S=p_{0}S+mg$

解得$p_{1}=1.05 \times 10^{5}\;\rm Pa$

可知在活塞到达卡扣前，气体做等压变化，则有$p_{2}=p_{1}=1.05 \times 10^{5}\;\rm Pa$

到达卡扣处后，气体做等容变化，由查理定律得$\dfrac{p_{2}}{T_{2}}=\dfrac{p_{3}}{T_{3}}$

解得$T_{2}=375\;\rm K$（或$t_{2}=102^\circ\rm C$）

缸内气体在整个过程中从外界吸收的热量$Q$。

$Q=25.25\\;\\rm J$

活塞从初始状态到卡扣处的过程中，做等压变化，则有$\dfrac{Sh}{T_{1}}=\dfrac{S\left( h+\Delta h \right)}{T_{2}}$

解得$\Delta h=5\;\rm cm$

因气体做等压变化，则外界对气体做功$W=−p_{1}S\Delta h=-5.25\;\rm J$

根据热力学第一定律有$\Delta U=W+Q$

解得$Q=25.25\;\rm J$