高中 | 洛伦兹力 题目答案及解析
稿件来源:高途
高中 | 洛伦兹力题目答案及解析如下,仅供参考!
选修3-1
第三章 磁场
3.5 运动电荷在磁场中受到的力
洛伦兹力
如图甲所示,圆心为$O$、半径为$R$的光滑绝缘圆管道固定放置在水平面上,$PM$为圆的条直径,在$P$点静止放置一质量为$m$、电荷量为$+q$的带电小球。$t=0$时刻开始,在垂直于圆管道平面的虚线同心圆形区域内加一随时间均匀变化的磁场,方向垂直纸面向里,磁感应强度大小随时间的变化如图乙所示,$t=t_{0}$时刻小球第一次运动到$M$点。下列说法正确的是$(\qquad)$
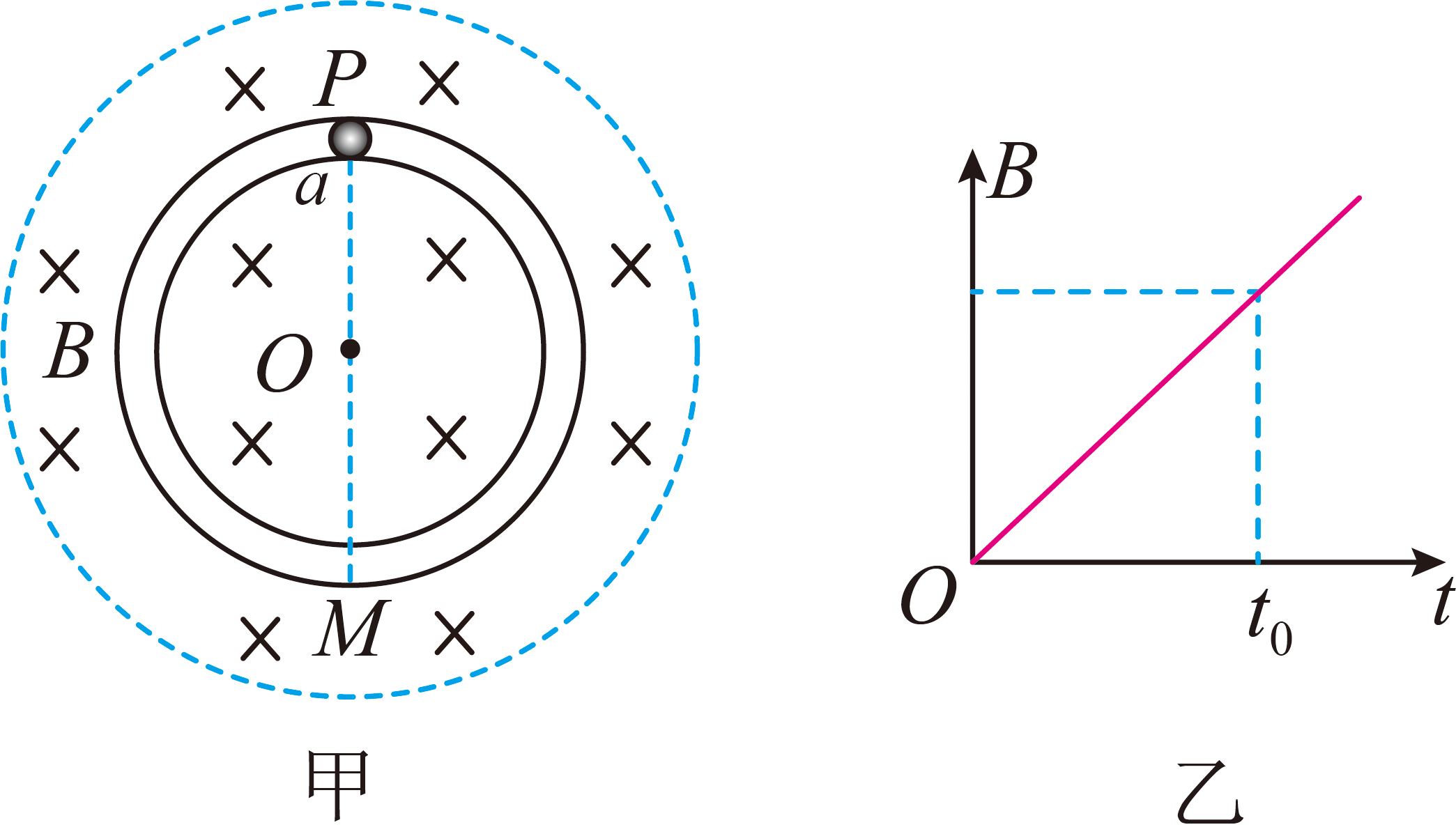
顺着磁感线方向看,小球沿顺时针方向运动
","$t_{0}$时刻磁感应强度的大小为$\\dfrac{2\\pi m}{qt_{0}}$
","管道内产生的感生电场强度大小为$\\dfrac{2\\pi mR}{qt_{0}^{2}}$
","$t_{0}$时刻小球对轨道的压力大小为$\\dfrac{2\\pi^{2}mR}{t_{0}^{2}}$
"]$\rm A$.磁场方向垂直纸面向里且随时间均匀增大,可知感生电场沿逆时针方向,小球带正电,所以在电场力作用下沿逆时针方向运动,故$\rm A$错误;
$\rm BC$.感生电场沿管道切线方向,小球在$0\sim t_{0}$时间内沿切线方向做加速运动,则有$qE_{感}=ma$,$\pi R=\dfrac{1}{2}at_{0}^{2}$
联立解得感生电场场强大小为$E_{感}=\dfrac{2\pi mR}{qt_{0}^{2}}$
根据法拉第电磁感应定律有$U=\dfrac{B}{t_{0}}\pi R^{2}$
又$E_{感}=\dfrac{U}{2\pi R}$
联立解得$t_{0}$时刻磁感应强度的大小为$B=\dfrac{4\pi m}{qt_{0}}$
故$\rm B$错误,$\rm C$正确;
$\rm D$.$t_{0}$时刻小球的速度大小为$v=at_{0}$
根据牛顿第二定律可得$qvB-N=m\dfrac{v^{2}}{R}$
联立解得$N=\dfrac{4\pi^{2}mR}{t_{0}^{2}}$
根据牛顿第三定律可知$t_{0}$时刻小球对轨道的压力大小为$\dfrac{4\pi^{2}mR}{t_{0}^{2}}$,故$\rm D$错误。
故选:$\rm C$。
高中 | 洛伦兹力题目答案及解析(完整版)
