某自助餐厅提供羊肉串，小王怕浪费每次最多只拿3串。已知他正好吃了10串，那么他共有多少种不同的拿法？

44

81

149

274

方法一：根据题意可知，小王每次只能拿1串、2串或3串，一共吃了10串。若有3次拿了3串，1次拿了1串，则一共取餐4次，即这4次取餐中有3次是拿了3串，有种不同的取餐情况。同理，不同拿法可列表如下：

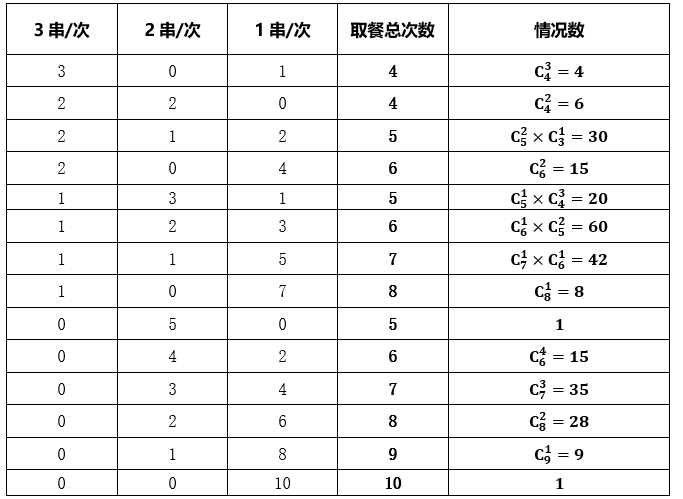
则所求总情况共有4+6+30+15+20+60+42+8+1+15+35+28+9+1=274种。

方法二：爬楼梯模型。本题可以理解为一共爬了10级台阶，每次可以爬1至3级。

先对简单情况进行讨论：

①爬上1级台阶，只有一次上了1级，共1种情况；

②爬上2级台阶，上楼梯的情况有（1，1）、（2），共2种情况；

③爬上3级台阶，上楼梯的情况有（1，$1$，1）、（1，2）、（2，1）、（3），共4种情况；

④爬上4级台阶，可以对最后一次上的台阶数进行分类讨论：

a.最后一次爬了3级，则需先爬了1级台阶，同①有1种情况；

b.最后一次爬了2级，则需先爬了2级台阶，同②有2种情况；

c.最后一次爬了1级，则需先爬了3级台阶，同③有4种情况；

所以爬4级台阶的情况数为a.b.c.三类情况数之和，即等于爬1级、2级、3级的情况数之和，共1+2+4=7种情况。

以此类推，由于最后一次可以爬1至3级台阶，所以爬上n（n＞3）级台阶情况数等于爬n-3级、n-2级、n-1级的情况数之和，则有：

爬上5级台阶的情况数等于爬2级、3级、4级的情况数之和，共2+4+7=13种情况；

爬上6级台阶的情况数等于爬3级、4级、5级的情况数之和，共4+7+13=24种情况；

爬上7级台阶的情况数等于爬4级、5级、6级的情况数之和，共7+13+24=44种情况；

爬上8级台阶的情况数等于爬5级、6级、7级的情况数之和，共13+24+44=81种情况；

爬上9级台阶的情况数等于爬6级、7级、8级的情况数之和，共24+44+81=149种情况；

爬上10级台阶的情况数等于爬7级、8级、9级的情况数之和，共44+81+149=274种情况，即题目所求情况为274种。

故本题选D。

【考场思维】因为每次最多能拿3串，所以最后一次取的串数只有3、2、1串，则前面几次需要取的串数应为7、8、9串，因此拿10串的方法数等于拿7串、8串、9串的情况数之和。观察选项数字A+B+C=D，大胆推测前三个选项分别为拿7串、8串、9串的情况数，则D项为答案。