如下图，AD=DE=EC，F是BC的中点，G是FC的中点，如果三角形ABC的面积是24，则三角形CEG的面积是：

2

3

4

6

作AM垂直于BC于M点，EN垂直BC于N点。

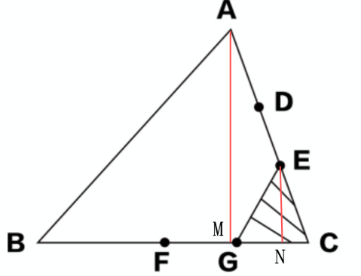
因为直角三角形AGC和直角三角形ENC共用∠C，所以两个直角三角形是相似三角形，对应边成比列，CE∶CA＝NE∶MA＝1∶3，则NE＝MA。因为三角形ABC的面积是24，所以BC×MA＝48。又因为“F是BC的中点，G是FC的中点”，所以CG∶BC＝1∶4，则CG＝BC。△ABC的面积＝×BC×AG，则△EGC的面积＝×GC×NE＝××BC××MA＝2。

故本题选A。