高中 | 速度选择器 题目答案及解析
稿件来源:高途
高中 | 速度选择器题目答案及解析如下,仅供参考!
选修3-1
第三章 磁场
3.6 带电粒子在匀强磁场中的运动
速度选择器
如图所示,直角坐标系第一象限内有一竖直分界线$PQ$,$PQ$左侧有一直角三角形区域$OAC$,其中分布着方向垂直纸面向里、磁感应强度为$B_{0}$的匀强磁场,已知$OA$与$y$轴重合,且$OA=a$,$\theta=60^\circ$,$C$点恰好处于$PQ$分界线上。$PQ$右侧有一长为$L$的平行板电容器,板间距为$a$,上极板与左侧磁场的上边界平齐,内部分布着方向垂直纸面向里、强弱随$y$坐标变化的磁场和竖直向下、电场强度大小为$E$的匀强电场。该复合场能使沿水平方向进入电容器的电子均能沿直线匀速通过电容器。在平行板电容器右侧某区域,存在一垂直纸面向里、磁感应强度为$2B_{0}$的匀强磁场(图中未画出),使水平通过平行板电容器的电子进入该磁场后汇聚于$x$轴上一点,现有速率不同的电子在纸面上从坐标原点$O$沿不同方向射到三角形区域,不考虑电子间的相互作用及电子的重力,已知电子的电量为$e$,质量为$m$。
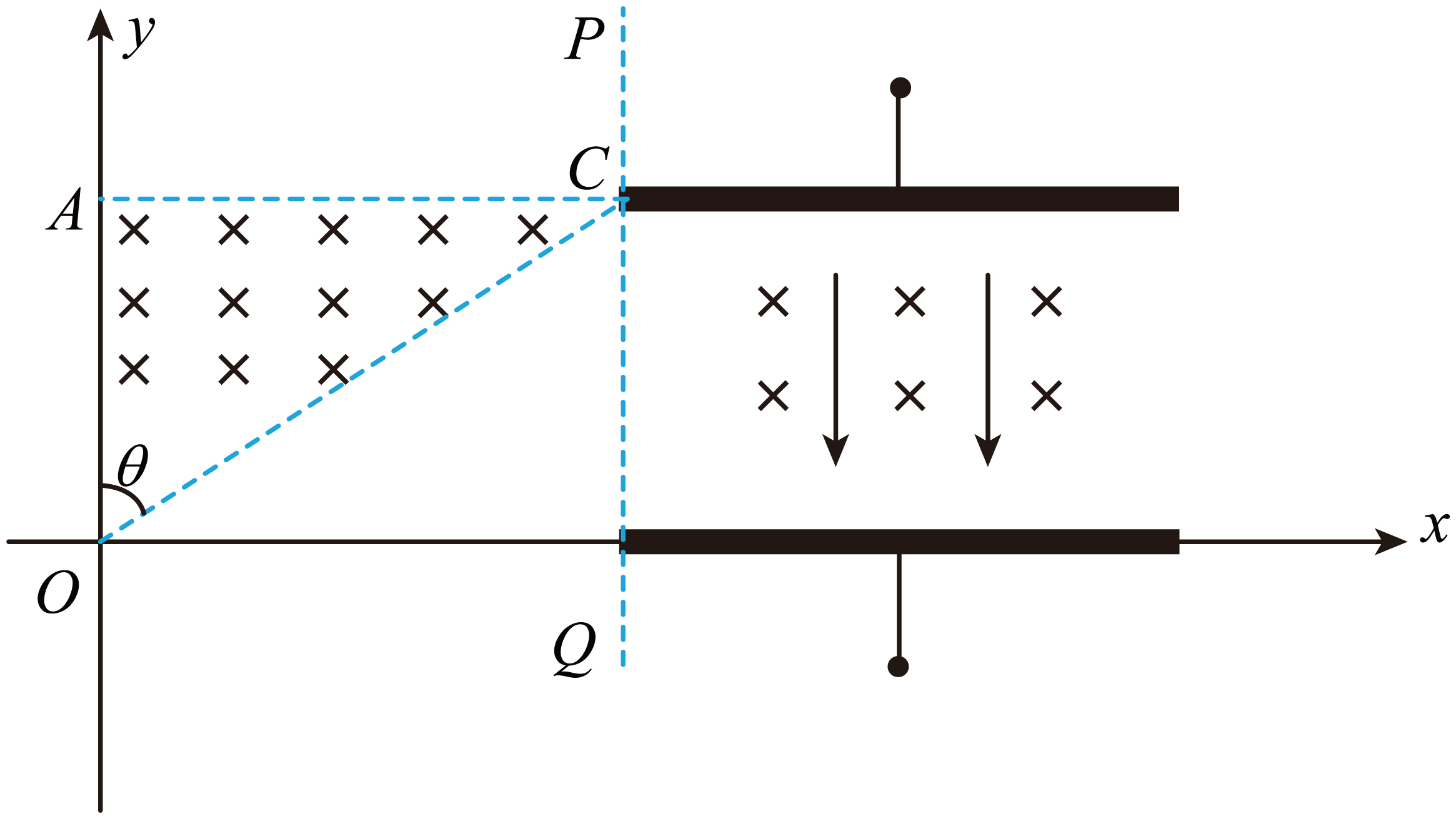
当速度方向沿$y$轴正方向时,求能进入平行板电容器的电子所具有的最大速度是多少;
$\\dfrac{eB_{0}a}{m}$
"]]根据题意可知,由洛伦兹力提供向心力,有$evB_{0}=m\dfrac{v^{2}}{r}$
解得$v=\dfrac{qB_{0}r}{m}$
可知能从$OC$边出磁场的电子,当运动轨迹和$AC$相切时半径最大,故半径最大值$r_{m}=a$
所以能从$OC$边出磁场的电子所具有的最大速度$v_{\text{m}}=\dfrac{eB_{0}a}{m}$
写出电容器内磁场的磁感应强度$B$随$y$坐标的变化规律;
$B=\\dfrac{mE}{2eB_{0}y}$
"]]根据题意,画出从$y$处水平进入平行板间的粒子的运动轨迹,如图所示
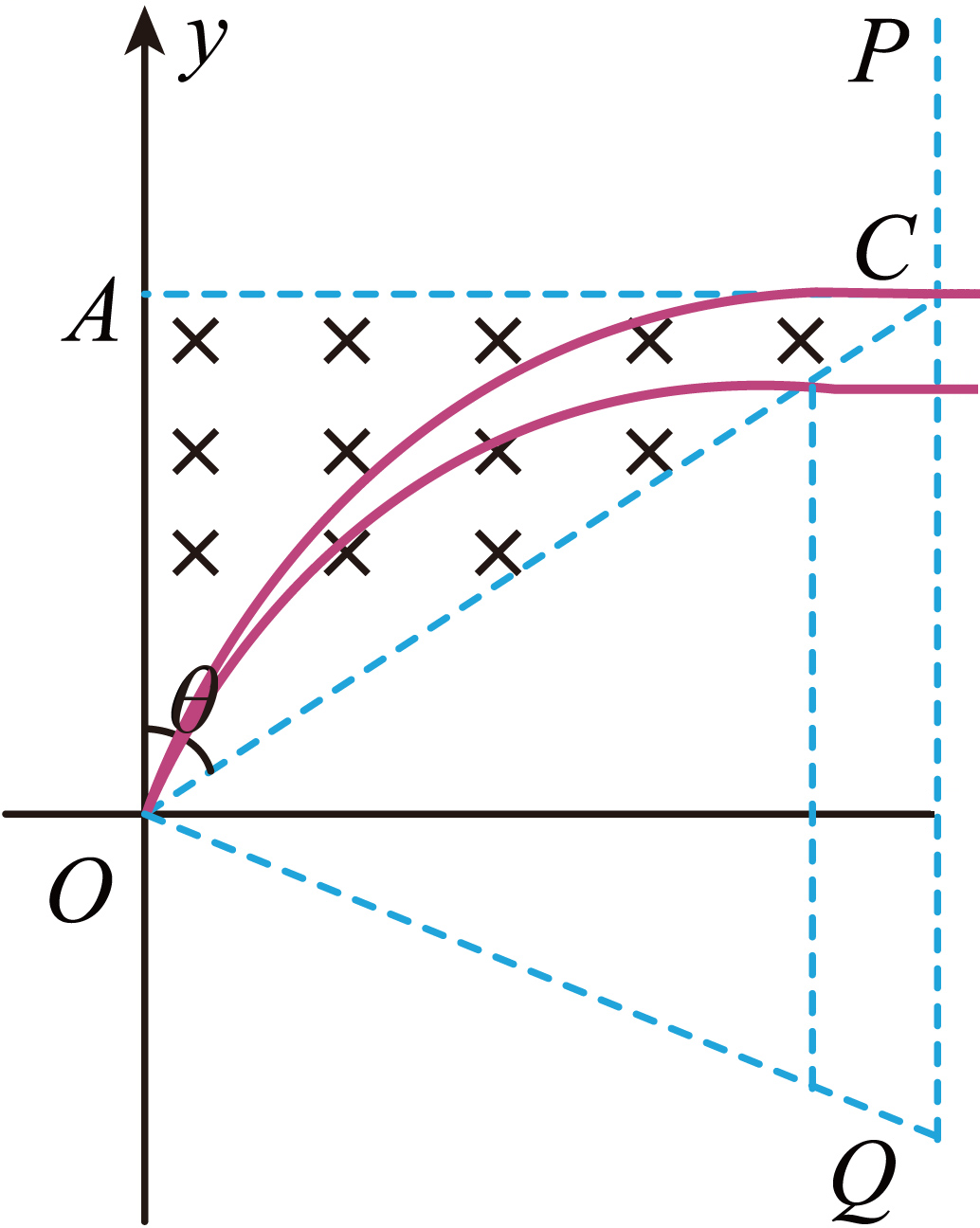
由几何关系可得,运动半径$r=2y$
可得$v=\dfrac{2eB_{0}y}{m}$
电子均能沿直线匀速通过电容器,则有$eE=evB$
解得$B=\dfrac{E}{v}=\dfrac{mE}{2eB_{0}y}$
若电子沿上极板边缘离开电容器后立即进入右侧磁场,求汇聚点的横坐标。
$\\sqrt{3}a+L+a$
"]]水平进入右侧磁场,因磁感应强度为$2B_{0}$,所以运动半径为$R=y$
磁场左边界为倾角$45^\circ$的斜线,如图所示
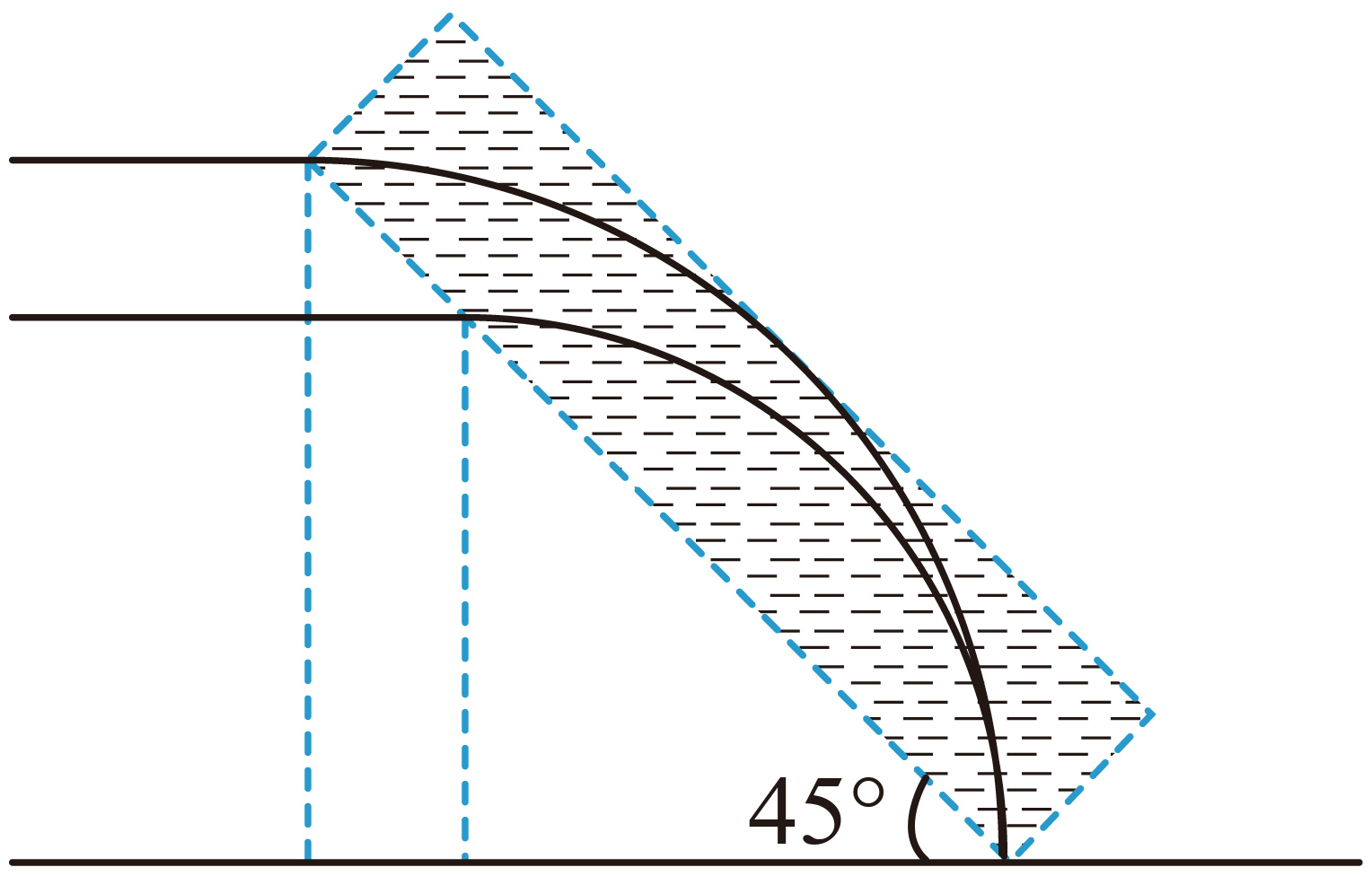
由几何关系可得,汇聚点横坐标$x=\sqrt{3}a+L+a$
高中 | 速度选择器题目答案及解析(完整版)
