高中 | 闭合电路的欧姆定律基本问题 题目答案及解析
稿件来源:高途
高中 | 闭合电路的欧姆定律基本问题题目答案及解析如下,仅供参考!
选修3-1
第二章 恒定电流
2.7 闭合电路的欧姆定律
闭合电路的欧姆定律基本问题
小明的外婆家养了许多的鹅,外公想通过人工方式将鹅蛋孵化出来,温度测量是其中一个重要的环节。小明想帮外公设计一个简易电子温度计,用来监测孵化箱中的温度,他从自己的实验套装中找到以下器材:
$\rm A$.热敏电阻(常温下阻值约为几千欧姆)一个;
$\rm B$.电流表(满偏电流为$300\;\rm \mu A$,内阻为$90\;\rm \Omega$);
$\rm C$.电阻箱(阻值范围为$0\sim 999.99\;\rm \Omega$);
$\rm D$.电阻箱(阻值范围为$0\sim 9999.9\;\rm \Omega$);
$\rm E$.滑动变阻器(最大阻值为$10\;\rm k\Omega$);
$\rm F$.电源一个(电动势为$3\;\rm V$,内阻不计);
$\rm G$.单刀双掷开关一个;
$\rm H$.单刀单掷开关一个;
$\rm I$.导线若干。
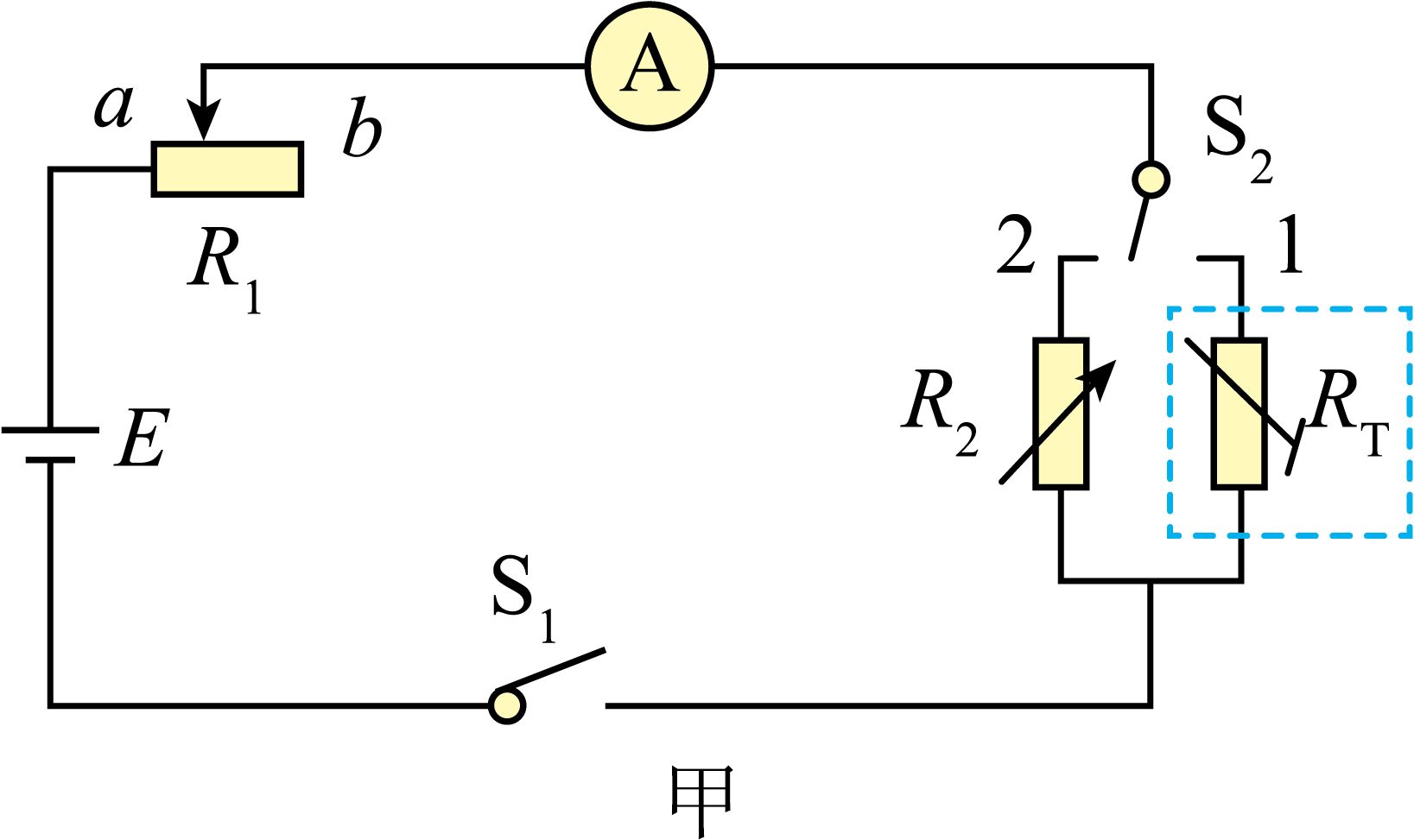
由于没有电压表,小明设计了如图甲所示电路来测量该热敏电阻在不同温度下的阻值,闭合开关$\rm S_{1}$前,应该将滑动变阻器$R_{1}$的滑片滑到 (填“$a$”或“$b$”)端,电阻箱$R_{2}$应该选 (填“$C$”或“$D$”)并调到最大值,将开关$\rm S_{2}$打到$1$位置。将热敏电阻$R_{T}$放至某温度下的水中,调节滑动变阻器$R_{1}$,让电流表达到接近满偏的值$I$,将开关$\rm S_{2}$打到$2$位置,逐渐减小电阻箱$R$接入电路的阻值,当电流表的示数再次为$I$时,此时电阻箱$R$的阻值就是此温度下热敏电阻$R_{T}$的阻值,重复此方法得到如下数据:
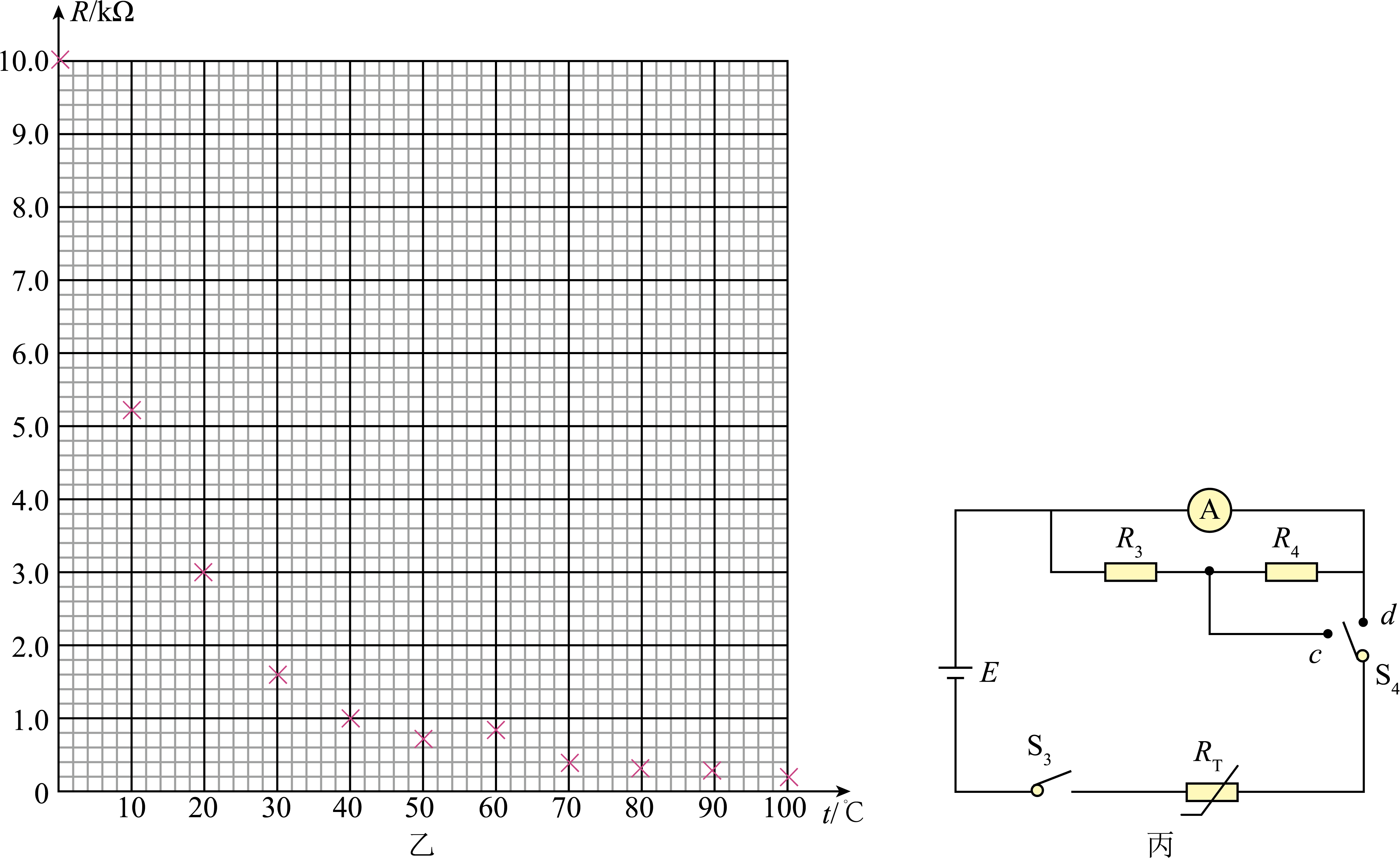
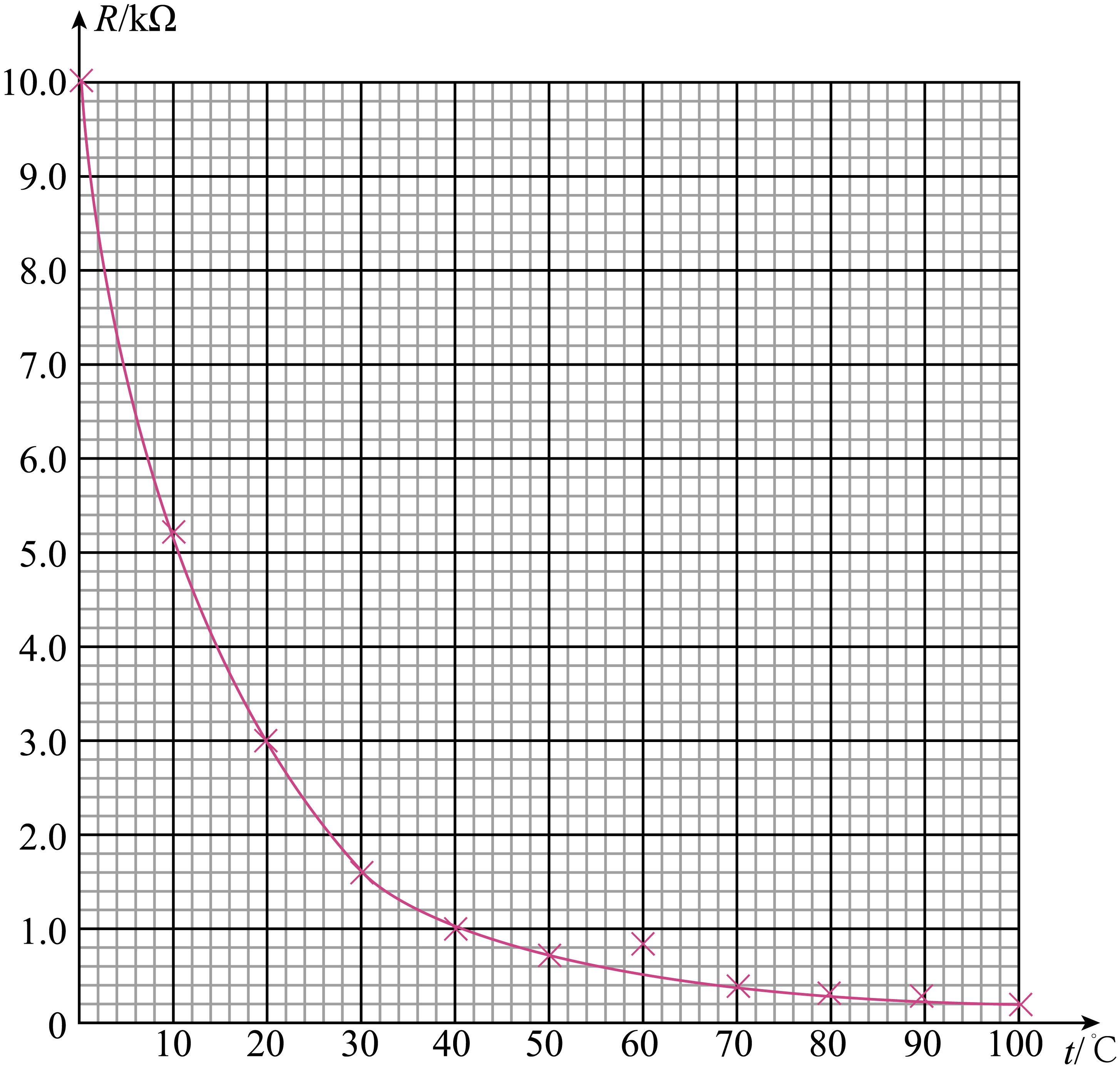
| 温度 | $0^\circ\rm C$ | $10^\circ\rm C$ | $20^\circ\rm C$ | $30^\circ\rm C$ | $40^\circ\rm C$ | $50^\circ\rm C$ | $60^\circ\rm C$ | $70^\circ\rm C$ | $80^\circ\rm C$ | $90^\circ\rm C$ | $100^\circ\rm C$ |
| 阻值$/\rm k\Omega$ | $9.99$ | $5.20$ | $3.00$ | $1.60$ | $1.00$ | $0.70$ | $0.83$ | $0.40$ | $0.31$ | $0.24$ | $0.20$ |
为防止电路中电流太大损坏电流表和电源,所以应该在闭合$S_{1}$前将$R_{l}$调到较大值位置,所以选$b$端。小明使用的是等效替代的思想测量热敏电阻的阻值,常温下为几千欧姆,所以$R_{2}$应选用$0\sim 9999.9\;\rm \Omega$的““$D$”电阻箱。
其中部分数据已经在如图乙所示的坐标纸上标出,请将剩余的点标上并描绘出热敏电阻$R_{T}$电阻随温度的变化曲线 。
见解析
"]]作图如下
小明又设计了一个如图丙所示的电路通过电流表的示数来推算温度,可实现$\rm 0\sim 100^\circ C、0\sim 40^\circ C$两种测量范围,其中$R_{3}=$ $\;\rm \Omega$(保留到小数点后$2$位),为了监测烧水壼内的水温,应该将开关$S_{4}$打到 (填“$c$”或“$d$”)位置。
由题意可知温度越高,$R_{T}$的阻值越小,通过电路的电流越大,两个档挡中的温度最大值分别对应$\rm 40^\circ C$和$\rm 100^\circ C$,对应阻值分别为$1\;\rm k\Omega$和$200\;\rm \Omega$,对应电流分别为$3\;\rm mA$和$15\;\rm mA$,所以,需要将现有电流表改装成具有两个量程的电流表。$\rm S_{4}$打向$c$时为大量程$0\sim 15\;\rm mA$档,对应温度为$\rm 0\sim 100^\circ C$,此时有$\dfrac{I_{g}}{I_{mc}-I_{g}}=\dfrac{R_{3}}{R_{g}+R_{4}}$
同理$\rm S_{4}$打向$d$时有$\dfrac{I_{g}}{I_{md}-I_{g}}=\dfrac{R_{3}+R_{4}}{R_{g}}$
代入数据得$R_{3}=2.00\;\rm \Omega$
$R_{4}=8.00\;\rm \Omega$
开水温度高达$100^\circ\rm C$,测量烧水壼内温度应该将开关$\rm S_{4}$打向$c$位置更准确。
高中 | 闭合电路的欧姆定律基本问题题目答案及解析(完整版)
