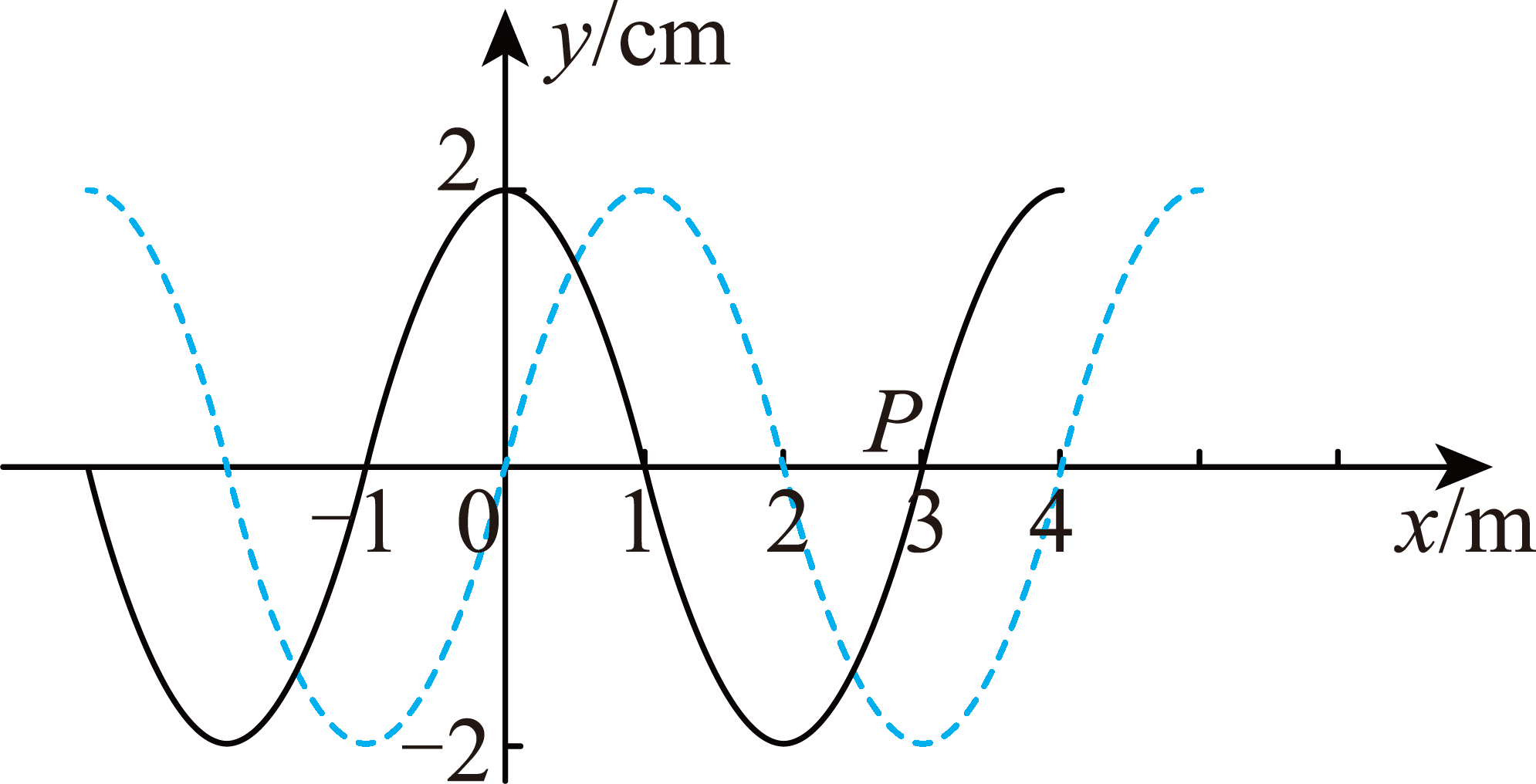
求该波在$0\sim 0.2\;\rm s$内传播的距离；

若该波沿$x$轴正方向传播，$\\left( n+\\dfrac{1}{4} \\right)\\lambda=(4n+ 1)\\;{\\rm m}\\left( n=0,\\text{1},\\text{2},\\cdots \\right)$；若该波沿$x$轴负方向传播，$\\left( n+\\dfrac{3}{4} \\right)\\lambda=\\left( 4n\\text{+3} \\right)\\ {\\rm m}\\left( n=0,\\text{1},\\text{2},\\cdots \\right)$

由题图可知，该波的波长$\lambda=4\;\rm m$

若该波沿$x$轴正方向传播，则该波在$\Delta t$时间内传播的最小距离$x=1\;\rm m$

由周期性可知，该波在$0\sim 0.2\;\rm s$内传播的距离$x_{1}=\left( n+\dfrac{1}{4} \right)\lambda=(4n+1)\;{\rm m}\left( n=0,\text{1},\text{2},\cdots \right)$

若该波沿$x$轴负方向传播，则该波在$\Delta t$时间内传播的最小距离$x{^\prime}=3\;\rm m$

由周期性可知，该波在$0\sim 0.2\;\rm s$内传播的距离$x_{2}=\left( n+\dfrac{3}{4} \right)\lambda=\left( 4n\text{+3} \right)\ {\rm m}\left( n=0,\text{1},\text{2},\cdots \right)$

若该波的波速大小$v=35\;\rm m/s$，请分析判断此波的传播方向，并求出质点$P$在$0\sim 0.2\;\rm s$内通过的路程。

$x$轴负方向；$14\\;\\rm cm$

若波速大小$v=35\;\rm m/s$，则该波的周期$T=\dfrac{\lambda}{v}=\dfrac{4}{35}\;\rm s$

因为$\Delta t=0.2\;\rm s=1\dfrac{3}{4}T$，所以波沿$x$轴负方向传播。

在$t=0$时刻，质点$P$处于平衡位置并沿$y$轴正方向运动，则在$t=0.2\;\rm s$时刻，质点$P$到达负方向的最大位移处，在$0\sim 0.2\;\rm s$内，质点$P$通过的路程$s=4A+3A=7A=7 \times 2\;\rm cm=14\;\rm cm$