用所测物理量的符号表示重力加速度的测量值，其表达式为$g=$                 ；

$n$次全振动所用的时间$t$，则单摆的周期为$T=\dfrac{t}{n}$

根据单摆的周期公式$T=2\pi\sqrt{\dfrac{l}{g}}$，可得重力加速度为$g=\dfrac{4\pi^{2}n^{2}l}{t^{2}}$

如果已知摆球直径为$2.00\;\rm cm$，让刻度尺的零点对准摆线的悬点，摆线竖直下垂。如图$1$所示，那么单摆摆长是                 $\rm cm$。如果测定了$40$次全振动是时间如图$2$中秒表所示，那么单摆的摆动周期是                 $\rm s$。

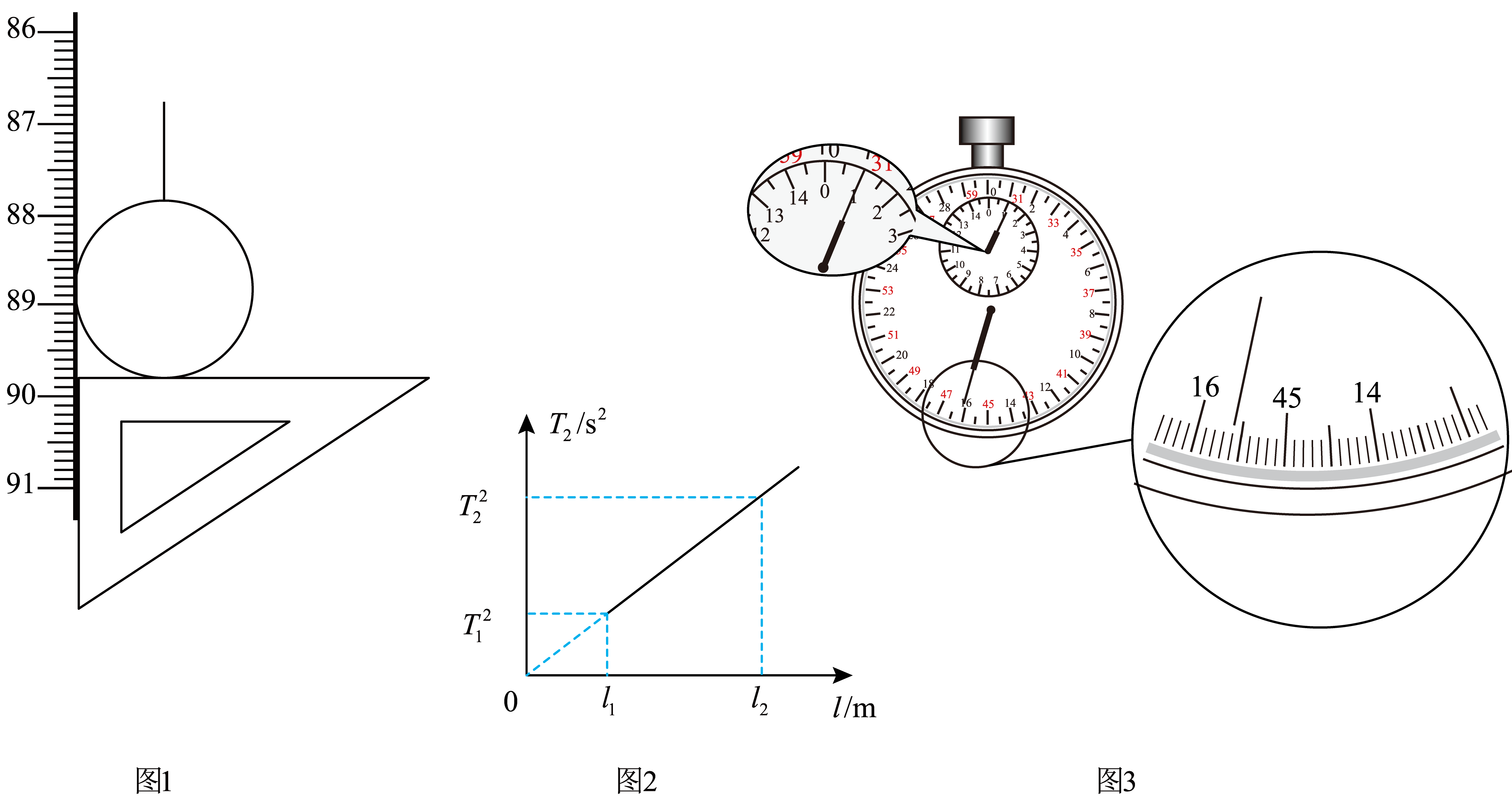
摆球下端的位置为$89.80\;\rm cm$，球心的位置为摆长，有

$89.80\;\rm cm-1.00\;\rm cm=88.80\;\rm cm$

$40$次全振动的时间由秒表读数为

$60\;\rm s+15.6\;\rm s=75.6\;\rm s$

则周期为$T=\dfrac{t}{n}=\dfrac{75.6}{40}\text{s}=1.89\;\rm \text{s}$

若测得的重力加速度数值大于当地的重力加速度的实际值，造成这一情况的原因可能是$(\quad\ \ \ \ )$。（选填下列选项前的序号）

测量摆长时，把摆线的长度当成了摆长

摆线上端未牢固地固定于$O$点，振动中出现松动，使摆线越摆越长

测量周期时，误将摆球$(n-1)$次全振动的时间$t$记为了$n$次全振动的时间，并由计算式$T=\\dfrac{t}{n}$求得周期

摆球的质量过大

$\rm A$．由$T=2\pi\sqrt{\dfrac{l}{g}}$可得$g=\dfrac{4\pi^{2}l}{T^{2}}$

把摆线的长度$l_{0}$当成了摆长，$l$变短，由上式可知，测得的$g$值偏小，故$\rm A$错误；

$\rm B$．摆线上端未牢固地固定于$O$点，振动中出现松动，使摆线变长，周期$T$变大，则$g$偏小，故$\rm B$错误；

$\rm C$．测量周期时，误将摆球（$n-1$）次全振动的时间$t$记成了$n$次全振动的时间，测出的周期$T$变小，则$g$偏大，故$\rm C$正确；

$\rm D$．单摆的周期与摆球的质量无关，质量过大不会改变周期，故$\rm D$错误。

故选：$\rm C$。

在与其他同学交流实验方案并纠正了错误后，为了减小实验误差，他决定用图像法处理数据，并通过改变摆长，测得了多组摆长$l$和对应的周期$T$，并用这些数据作出$T^{2}-l$图像如图$3$所示。图线斜率的意义                。

$\\dfrac{g}{4\\pi^{2}}$

$\\dfrac{4\\pi^{2}}{g}$

$g$

$\\dfrac{1}{g}$

根据单摆的周期公式$T=2\pi\sqrt{\dfrac{l}{g}}$，可得$T^{2}=\dfrac{4\pi^{2}}{g} \cdot l$

故$T^{2}-l$图像的斜率$k=\dfrac{4\pi^{2}}{g}$。

故选：$\rm B$。

在题④中，利用图线上任意两个点$a$、$b$的坐标$(l_{1}, T_{1}^{2})$、$(l_{2}, T_{2}^{2})$计算重力加速度的公式是                 。

$T^{2}-l$图像的斜率为$\dfrac{4\pi^{2}}{g}=\dfrac{T_{2}^{2}-T_{1}^{2}}{l_{2}-l_{1}}$

解得重力加速度为$g=\dfrac{4\pi^{2}\left( l_{2}-l_{1} \right)}{T_{2}^{2}-T_{1}^{2}}$

在题④中，如果在描点时若误将摆线长当做摆长，那么画出的直线将不通过原点，由图线斜率得到的重力加速度与正常相比，将产生哪一种结果？$(\quad\ \ \ \ )$

不变

偏大

偏小

都有可能

描点时若误将摆线长当作摆线长，那么画出的直线将不通过原点$T^{2}=\dfrac{4\pi^{2}}{g}\left(L_{线}+\dfrac{d}{2}\right)$

即作出$T^{2}-L_{线}$的图像，斜率不变，由图线斜率得到的重力加速度与原来相比，其大小不变。

故选：$\rm A$。