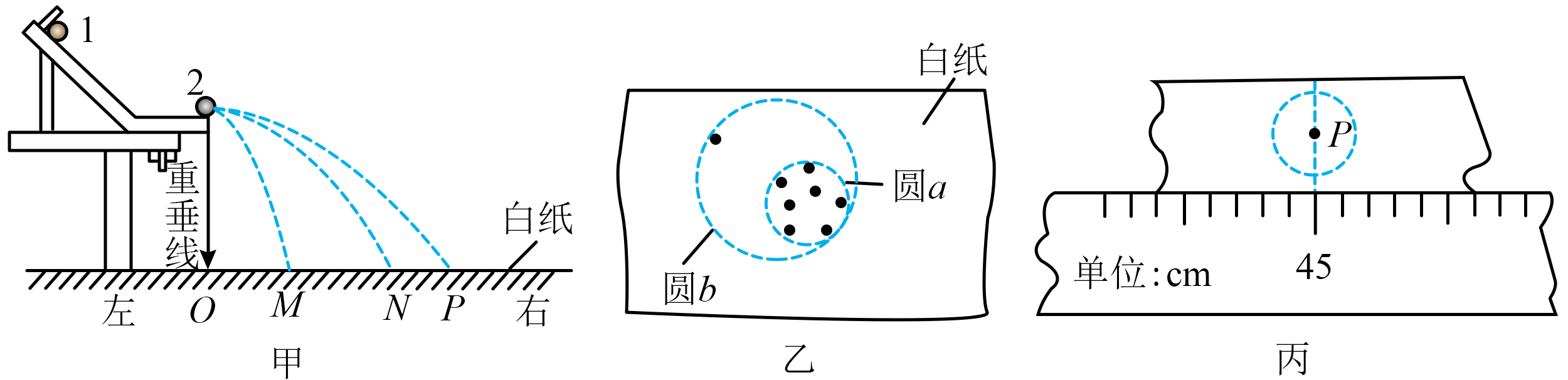
用“画圆法”确定小球$1$在没有与小球$2$发生碰撞时的平均落点$N$，则图乙中圆                   （填“$a$”或“$b$”）更合理。

用画圆法确定小球落地点时，需要用尽量小的圆把所有落点圈起来，圆心即为小球的平均落地点，个别偏离较远的点舍去，则图乙中圆$a$更合理。

关于实验操作和过程，下列说法正确的是$(\quad\ \ \ \ )$

实验时需测量小球开始释放时距离斜槽末端的高度$h$

实验装置中的铅垂线是用来判断斜槽末端是否水平的

实验时每次释放钢球$\\rm A$的位置必须相同，斜槽是否光滑对实验结果无影响

A．本实验实际是要测量小球的速度，由装置可以确定本实验采用平抛运动规律测量速度，考虑到所有小球平抛运动下落高度相同，运动时间相同，故只需要测量水平位即可用以代替平抛初速度，故不需要测量小球开始释放时距离斜槽末端的高度h，故A错误；

B．实验装置中的铅垂线是一方面是用来判断斜槽末端是否水平，另一方面也是用以确定初始位置，故B错误；

C．实验时每次释放钢球A的位置必须相同，只要释放位置相同斜槽是否光滑对小球到达斜槽末端时的速度无影响，对实验结果无影响，故C正确。

故选C。

本实验中用于验证动量守恒定律的表达式应为：${{m}_{1}}\cdot ON=$                    （用${{m}_{1}}$、${{m}_{2}}$、$OP$、$OM$表示）。

小球离开桌面后做平抛运动，抛出点的高度相同，则运动时间相同，设为$t$，不放小球$2$时，设小球$1$平抛运动初速度为$v_{0}$，小球$1$水平方向上有$ON={{v}_{0}}t$

解得${{v}_{0}}=\dfrac{ON}{t}$，放小球$2$时，设碰撞之后小球$1$、$2$速度分别为$v_{1}$、$v_{2}$，水平方向上有$OM={{v}_{1}}t$，$OP={{v}_{2}}t$，解得${{v}_{1}}=\dfrac{OM}{t}$，${{v}_{2}}=\dfrac{OP}{t}$，要验证动量守恒定律，则要验证${{m}_{1}}{{v}_{0}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}$，将速度代入上式化简得${{m}_{1}}\cdot ON={{m}_{1}}\cdot OM+{{m}_{2}}\cdot OP$。

刻度尺的零点与$O$点对齐，由图丙读得$OP=$                   $\rm cm$，又测得$ON=44.20\ \text{cm},OM=13.50\ \text{cm}$。将数据代入动量守恒表达式，计算得到碰撞前系统总动量$P$与碰撞后系统总动量${P}'$的误差$\dfrac{\mid P-{P}'\mid }{P}\times 100\%=$                  （计算结果保留$2$位有效数字），由此可判断该系统碰撞过程动量守恒。

刻度尺的最小分度是$\rm 1\ mm$，刻度尺的零点与$O$点对齐，由图丙读得$OP=45.00\operatorname{cm}$。

碰撞前系统总动量$P$与碰撞后系统总动量${P}'$的误差$\dfrac{\mid P-{P}'\mid }{P}\times 100\text{ }\!\!\%\!\!\text{ }=\dfrac{\left| 30\times 44.20-\left( 30\times 13.50+20\times 45.00 \right) \right|}{30\times 44.20}\times 100\text{ }\!\!\%\!\!\text{ }=1.6\text{ }\!\!\%\!\!\text{ }$

如图甲，若实验小组在记录投影点$O$后，由于失误将白纸水平向右移动了一段距离，再进行步骤（ⅲ）（ⅳ）（ⅴ），则计算得到的碰撞前系统的总动量                 （选填“大于”“等于”或“小于”）碰撞后的总动量。

如图甲，若实验小组在记录投影点$O$后，由于失误将白纸水平向右移动了一段距离，则测量的小球的水平位移都变小，再进行步骤（ⅲ）（ⅳ）（ⅴ），设白纸水平向右移动的距离为$x$，则碰撞前系统的总动量减小$\Delta p={{m}_{1}}x$

碰撞后系统的总动量减小$\text{ }\!\!\Delta\!\!\text{ }{p}'=\left( {{m}_{1}}+{{m}_{2}} \right)x$

则$\Delta p\lt \Delta {{p}^{'}}$

可知$p-\Delta p\gt {{p}^{'}}-\Delta {{p}^{'}}$

所以计算得到的碰撞前系统的总动量大于碰撞后的总动量。