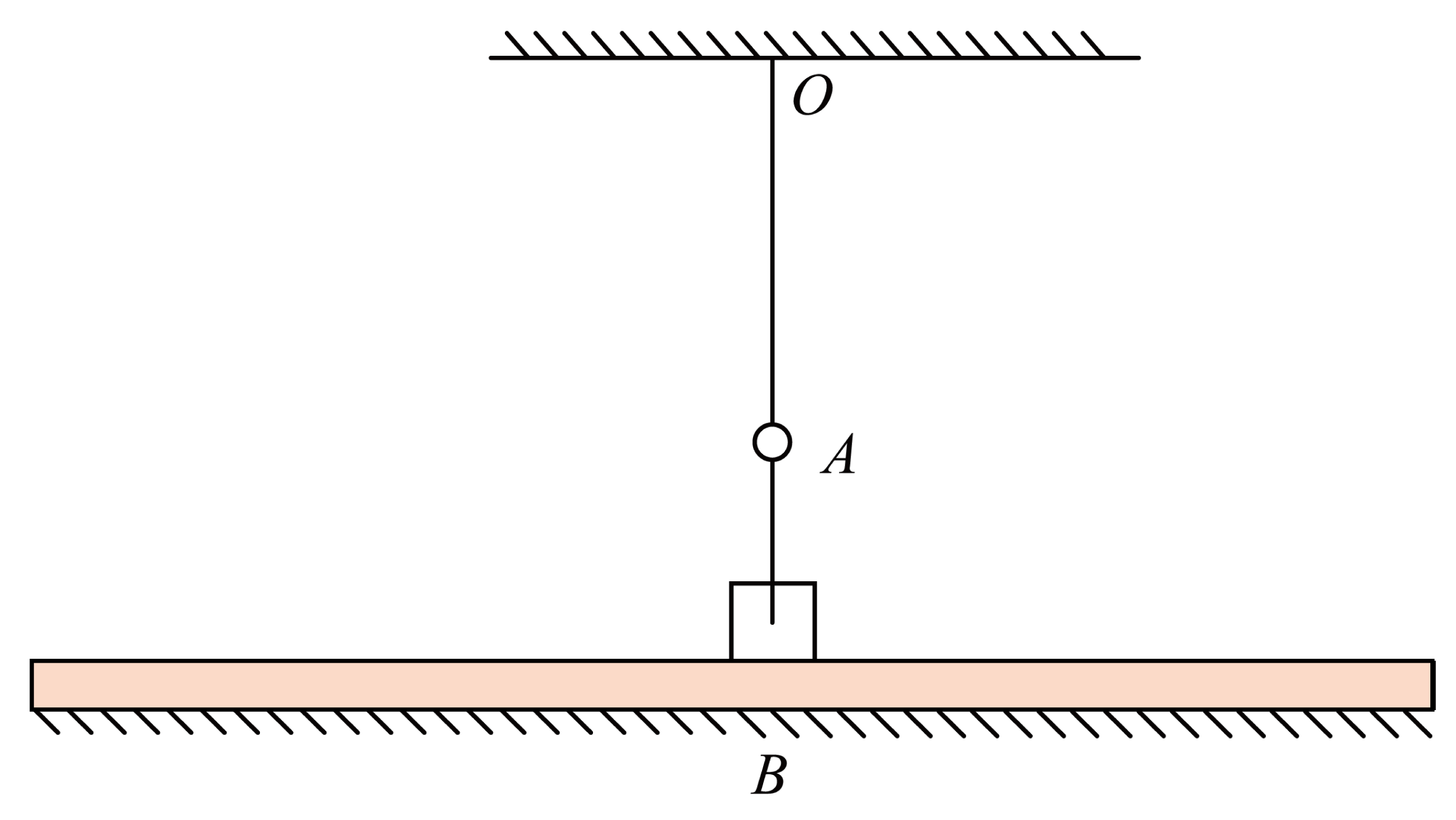
$v$为何值时，滑块到达某处时将与木板出现相对滑动，并求此位置与$B$的距离。

$v\\gt 2\\;\\rm m/s$，$0.4\\;\\rm m$

当木板和滑块刚好出现相对运动时，滑块中心到$A$点的距离为$L$，位移为$x_{1}$，弹性绳的弹力大小为$F$，弹性绳与竖直方向的夹角为$\theta$，如下图所示

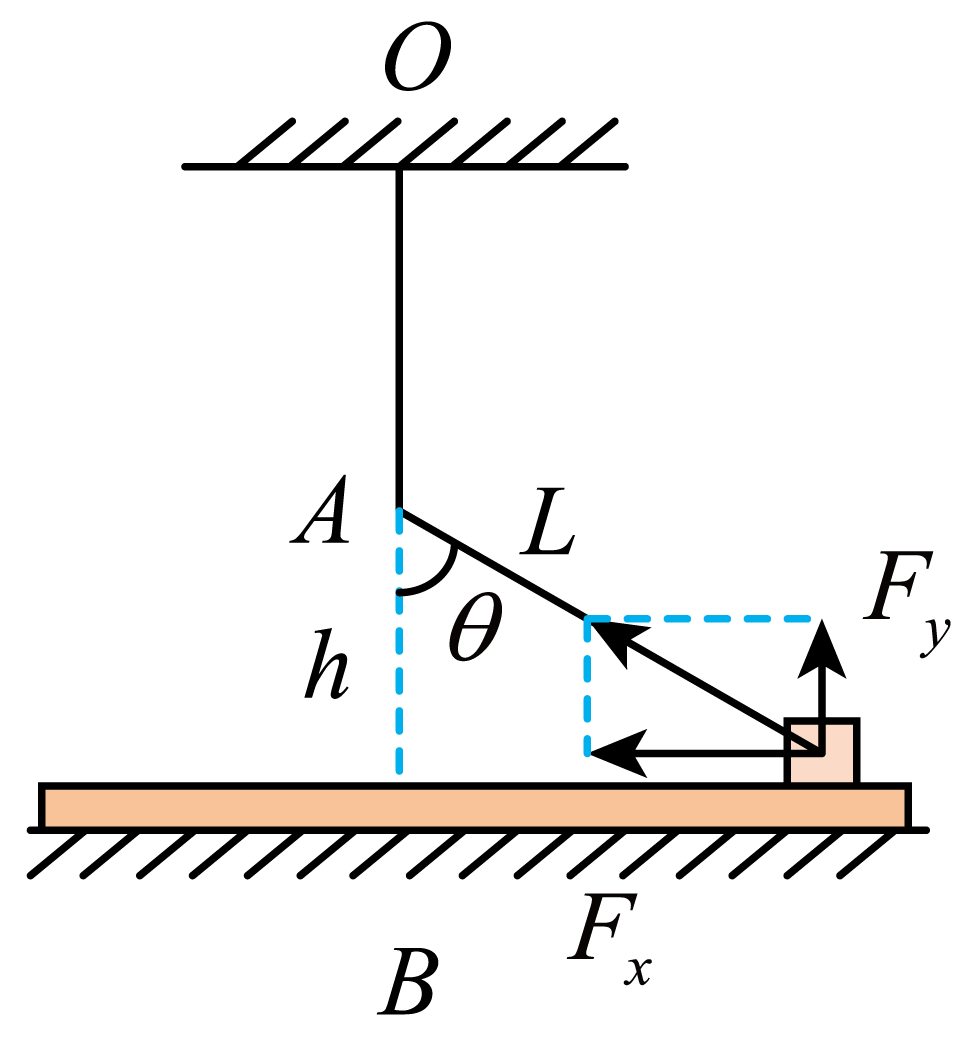
弹性绳弹力的水平分力$F_{x}=kL\sin \theta=kx_{1}$

弹性绳弹力的竖直分力$F_{y}=kL\cos \theta=kh=100 \times 0.1\;\rm N=10\;\rm N$

对滑块，有$F_{N}+F_{y}=Mg$

对整体，有$F_{x}=(M+m)a$

对木板，有$f=ma$

其中$f=\mu F_{N}=\mu (Mg-F_{y})=10\;\rm N$

联立求得$x_{1}=0.4\;\rm m$

即出现相对滑动的位置与$B$的距离为$0.4\;\rm m$。

根据机械能守恒定律，有$\dfrac{1}{2}kL^{2}-\dfrac{1}{2}kh^{2}=\dfrac{1}{2}(m+M){v_{1}}^{2}$

即$\dfrac{1}{2}k{x_{1}}^{2}=\dfrac{1}{2}(m+M){v_{1}}^{2}$

求得$v_{1}=2\;\rm m/s$

即$v\gt v_{1}=2\;\rm m/s$时滑块到达某处时将与木板出现相对滑动。

若$v= 2\sqrt{3}\;\rm \text{m}/\text{s}$，在刚好出现相对滑动时，使木板的速度瞬间变为$0$且固定不动，求此后滑块向右运动距$B$点的最大距离。

$0.6\\;\\rm m$

因为$v=2\sqrt{3}\;\rm \text{m}/s\gt 2\;\rm m/s$

设滑块和木板刚好出现相对滑动时的共同速度为$v_{2}$，根据机械能守恒定律，有$\dfrac{1}{2}k{x_{2}}^{2}=\dfrac{1}{2}(m+M)v^{2}-\dfrac{1}{2}(m+M)v_{2}^{2}$

其中$x_{2}=x_{1}=0.4\;\rm m$

求得$v_{2}=2\sqrt{2}\;\rm m/s$

此后木板停止运动，物块相对木板向右滑动，以向右为正方向，设滑块速度为零时相对$B$点的位移为$x_{3}$，根据能量守恒定律，有$\dfrac{1}{2}kx_{3}^{2}-\dfrac{1}{2}kx_{2}^{2}+f\left( x_{3}-x_{2} \right)=\dfrac{1}{2}M{v_{2}}^{2}$

解得$x_{3}=0.6\;\rm m$（另一解$x_{3}=-0.8\;\rm m$不合理，舍去）

故滑块向右运动距$B$点的最大距离为$0.6\;\rm m$。

（$2$）问条件下滑块在木板上滑动因摩擦而产生的热量。

$20\\;\\rm J$

因$kx_{3}=100 \times 0.6\;{\rm N=60\;\rm N}\gt f=10\;\rm N$

故滑块不能静止而向左滑动。

设向右为正方向，设滑块向左滑动直至速度再次为零时相对$B$点的位移为$x_{4}$，根据能量守恒定律，有$\dfrac{1}{2}kx_{3}^{2}-\dfrac{1}{2}kx_{4}^{2}=f\left( x_{3}-x_{4} \right)$

解得$x_{4}=-0.4\;\rm m$（另一解$x_{4}=0.6\;\rm m$不合理，舍去）

负号说明滑块位于$B$点左侧$0.4\;\rm m$处，因$k|x_{4}|=100 \times 0.4\;{\rm N=40\;\rm N}\gt f=10\;\rm N$

故滑块不能静止而向右运动。

同理，对滑块再向右运动直至速度为零的过程，有$\dfrac{1}{2}kx_{4}^{2}-\dfrac{1}{2}kx_{5}^{2}=f\left( x_{5}-x_{4} \right)$

解得$x_{5}=0.2\;\rm m$（另一解$x_{5}=-0.4\;\rm m$不合理，舍去）

因$kx_{5}=100 \times 0.2\;{\rm N=20\;\rm N}\gt f=10\;\rm N$

故滑块不能静止而向左运动。

同理，对滑块再向左运动直至速度为零的过程，有$\dfrac{1}{2}kx_{5}^{2}-\dfrac{1}{2}kx_{6}^{2}=f\left( x_{5}-x_{6} \right)$

解得$x_{6}=0$（另一解$x_{6}=0.2\;\rm m$不合理，舍去）

故滑块最终静止于$B$点。

在木板固定不动直至滑块停止运动的整个过程中，设滑块与木板摩擦产生的热量为$Q$，根据能量守恒定律，有$Q=\dfrac{1}{2}k{x_{2}}^{2}+\dfrac{1}{2}M{v_{2}}^{2}=\left\lbrack \dfrac{1}{2} \times 100 \times {0.4}^{2}+\dfrac{1}{2} \times 3 \times \left( 2\sqrt{2} \right)^{2} \right\rbrack\ \text{J}=20\;\rm \text{J}$