高中 | 带电粒子在匀强电场中的偏转运动 题目答案及解析
稿件来源:高途
高中 | 带电粒子在匀强电场中的偏转运动题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
带电粒子在匀强电场中的偏转运动
目前,我国正在集中力量开发芯片技术,而离子注入是其中一道重要的工序。如图所示是离子注入工作原理示意图,离子经加速后沿水平方向进入速度选择器,然后通过磁分析器,选择出特定比荷的离子,经偏转系统后注入处在水平面内的晶圆(硅片)。速度选择器和磁分析器中的匀强磁场的磁感应强度大小均为$B$,方向均垂直纸面向外;速度选择器和偏转系统中的匀强电场场强大小均为$E$,方向分别为竖直向上和垂直纸面向外。磁分析器截面是内外半径分别为$R_{1}$和$R_{2}$的四分之一圆环,其两端中心位置$M$和$N$处各有一个小孔;偏转系统中电场的分布区域是一边长为$L$的正方体,其底面与晶圆所在水平面平行。当偏转系统不加电场时,离子恰好竖直注入到晶圆上的$O$点。整个系统置于真空中,不计离子重力。求:
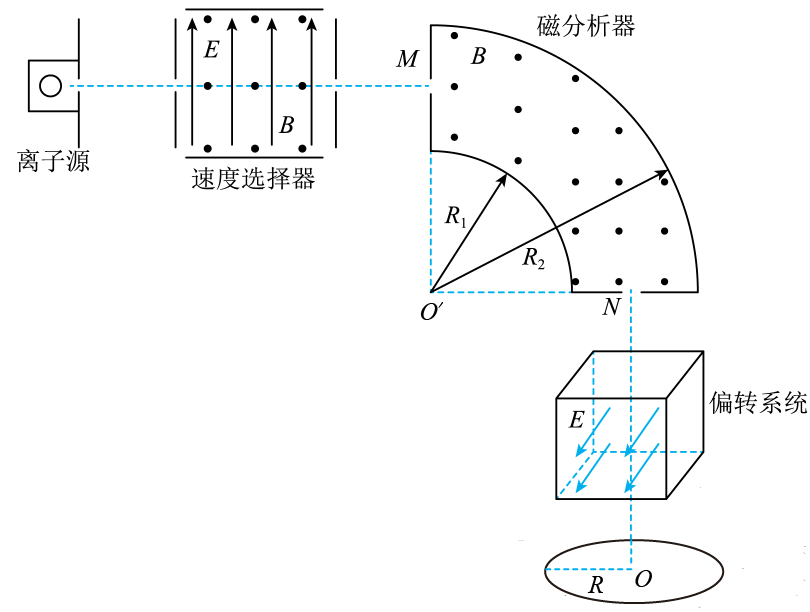
判断离子的电性和离子通过速度选择器的速度大小$v$;
带正电;$v= \\dfrac{E}{B}$ ;
"]]由离子通过速度选择器时可知,离子带正电$Eq=Bqv$
解得速度$v=\dfrac{E}{B}$
磁分析器选择出来离子的比荷$\dfrac{q}{m}$;
$\\dfrac{q}{m}= \\dfrac{2E}{(R_{1}+R_{2})B^{2}}$;
"]]离子在磁分析器中,有$qvB=m\dfrac{v^{2}}{R}$
由几何关系,可得$R=\dfrac{R_{1}+R_{2}}{2}$
联立解得$\dfrac{q}{m}=\dfrac{2E}{(R_{1}+R_{2})B^{2}}$
偏转系统加电场时,离子从偏转系统底面飞出,若晶圆所在的水平面是半径为$\dfrac{3L^{2}}{R_{1}+ R_{2}}$的圆面,为了使偏转粒子能打到晶圆的水平面上,晶圆平面到偏转系统的距离满足什么条件?
$\\dfrac{3L^{2}}{R_{1}+R_{2}}- \\dfrac{L}{2}$
"]]偏转系统加电场 $E$时,离子在电场中做类平抛运动后在真空中做匀速直线运动,若偏转系统距离晶圆的距离为$H$,当离子恰从偏转系统的立方体边缘射出时,偏转角最大,打在圆晶上的距离最远,此时偏转角满足$\tan\alpha=2 \times \dfrac{y_{\parallel}}{x_{\perp}}=2 \times \dfrac{\dfrac{L}{2}}{L}=1$
(即速度方向与位移方向的关系$\tan\alpha=2\tan\theta$)
打在晶圆上的最远距离为$R=\left(\dfrac{L}{2}+H\right)\tan\alpha$
由题意可知$R=\dfrac{3L^{2}}{R_{1}+R_{2}}$
解得$H=\dfrac{3L^{2}}{R_{1}+R_{2}}-\dfrac{L}{2}$
高中 | 带电粒子在匀强电场中的偏转运动题目答案及解析(完整版)
