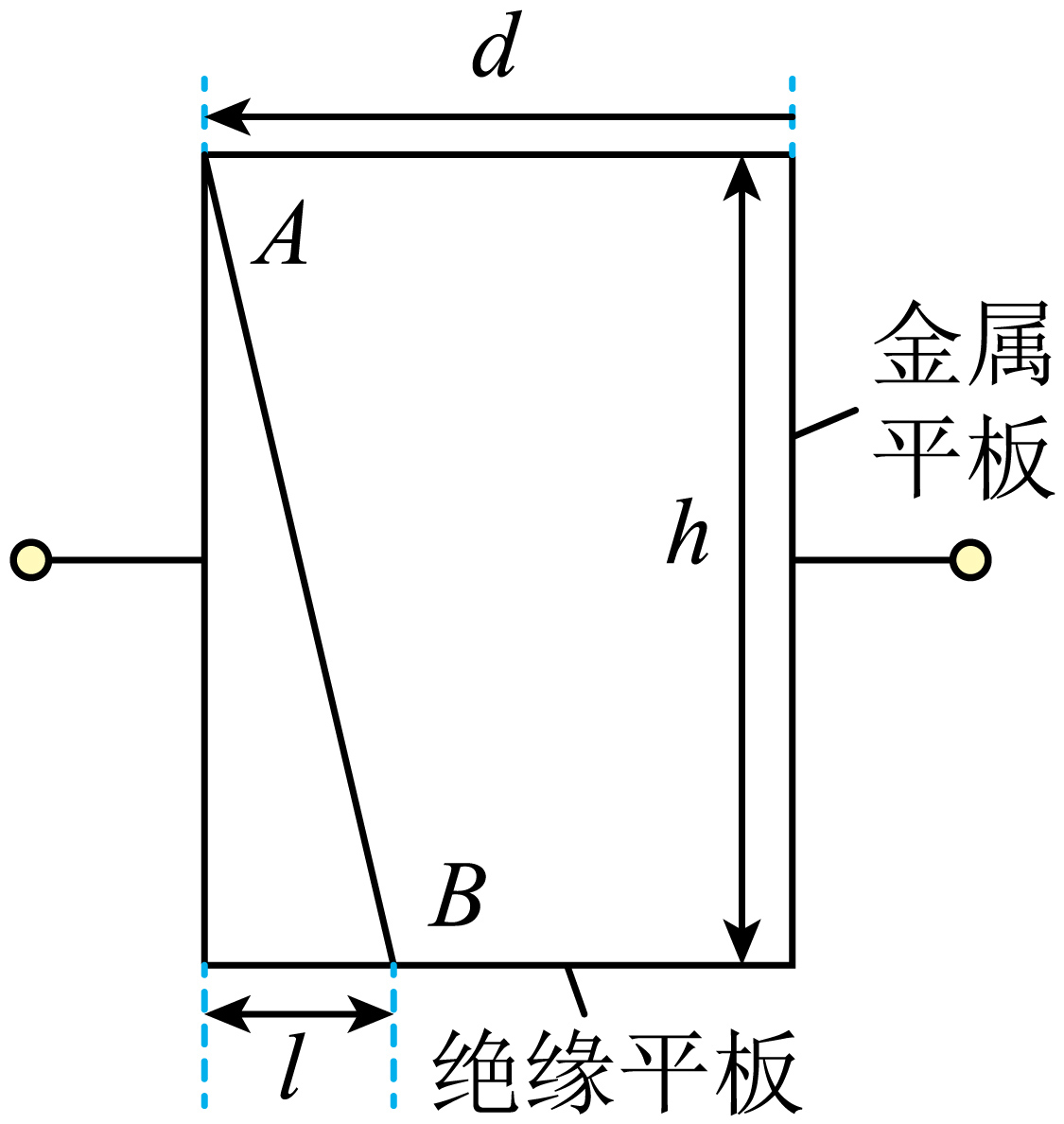
颗粒碰撞前的电荷量$q$。

$q=\\dfrac{mgdl}{Uh}$

根据题意可知，颗粒在竖直方向上做自由落体，则有$h=\dfrac{1}{2}gt^{2}$

水平方向上做匀加速直线运动，则有$\dfrac{qU}{d}=ma$，$l=\dfrac{1}{2}at^{2}$

解得$q=\dfrac{mgdl}{Uh}$

颗粒在$B$点碰撞后的电荷量$Q$。

$Q=\\dfrac{kmgdh}{Ul}$

根据题意可知，颗粒与绝缘板第一次碰撞时，竖直分速度为$v_{y1}=\sqrt{2gh}$

水平分速度为$v_{x1}=\sqrt{2al}=\sqrt{\dfrac{2gl^{2}}{h}}$

则第一次碰撞后竖直分速度为$v_{y2}=kv_{y1}=k\sqrt{2gh}$

设第一次碰撞后颗粒速度方向与水平方向夹角为$\theta$，则有$\tan\theta=\dfrac{v_{y2}}{v_{x1}}=\dfrac{kh}{l}$

由于第一次碰撞后瞬间颗粒所受合力与速度方向垂直，则有$\tan\theta=\dfrac{\dfrac{UQ}{d}}{mg}=\dfrac{UQ}{mgd}$

联立解得$Q=\dfrac{kmgdh}{Ul}$

颗粒从$A$点开始运动到第二次碰撞过程中，电场力对它做的功$W$。

若$(4k+1)l+\\dfrac{4k^{3}h^{2}}{l} \\leqslant d$时，$W=\\dfrac{mgl^{2}}{h}+ 4k^{2}mgh+\\dfrac{4k^{4}mgh^{3}}{l^{2}}$，若$(4k+1)l+\\dfrac{4k^{3}h^{2}}{l} \\gt d$时，$W=\\dfrac{mgl^{2}}{h}+ \\dfrac{kmgh(d-l)}{l}$

根据题意可知，由于$k\lt1$，则第一次碰撞后颗粒不能返回上绝缘板，若颗粒第二次碰撞是和下绝缘板碰撞，设从第一碰撞后到第二次碰撞前的运动时间为$t'$，则有$t'=\dfrac{2k\sqrt{2gh}}{g}= 2k\sqrt{\dfrac{2h}{g}}$

水平方向上做匀加速直线运动，加速度为$a'=\dfrac{UQ}{md}=\dfrac{kgh}{l}$

水平方向运动的距离为$l'=v_{x1}t'+\dfrac{1}{2}a{t}'^{2}=4kl+\dfrac{4k^{3}h^{2}}{l}$

则电场对颗粒做的功为$W=\dfrac{Uql}{d}+\dfrac{UQl'}{d}=\dfrac{mgl^{2}}{h}+4k^{2}mgh+\dfrac{4k^{4}mgh^{3}}{l^{2}}$

若$l+l^\prime\gt d$，则颗粒第二次碰撞是和右侧金属板碰撞，则颗粒从第一次碰撞到第二次碰撞过程中水平方向位移为$d-l$，颗粒从$A$点开始运动到第二次碰撞过程中，电场对颗粒做的功为$W'=\dfrac{Uql}{d}+\dfrac{UQ(d-l)}{d}=\dfrac{mgl^{2}}{h}+\dfrac{kmgh(d-l)}{l}$