高中 | 牛顿第二定律的两类基本问题 题目答案及解析
稿件来源:高途
高中 | 牛顿第二定律的两类基本问题题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.6 用牛顿运动定律解决问题(一)
牛顿第二定律的两类基本问题
如图,在$xOy$平面第一、四象限内存在垂直平面向里的匀强磁场,磁感应强度大小为$B$,一带正电的粒子从$M(0, −y_{0})$点射入磁场,速度方向与$y$轴正方向夹角$\theta=30^\circ $,从$N(0, y_{0})$点射出磁场。已知粒子的电荷量为$q(q \gt 0)$,质量为$m$,忽略粒子重力及磁场边缘效应。
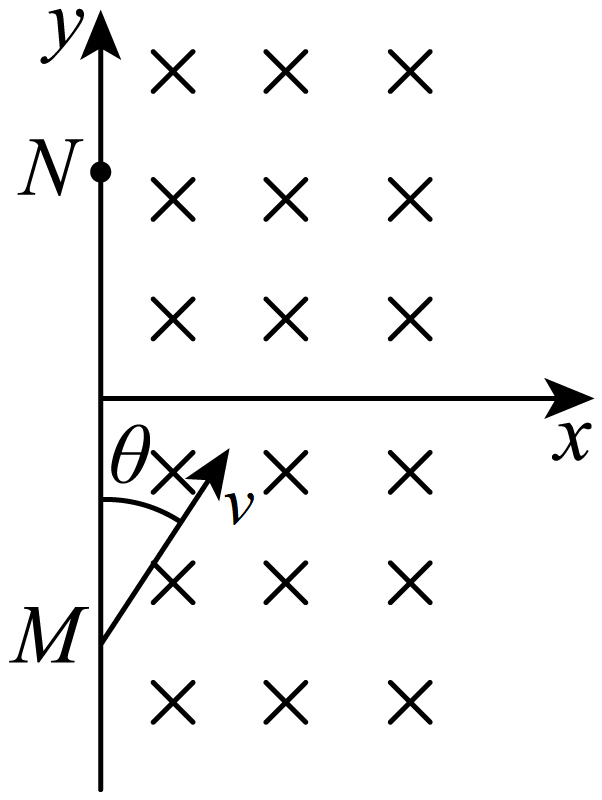
求粒子射入磁场的速度大小$v_{1}$和在磁场中运动的时间$t_{1}$;
$\\dfrac{2qBy_{0}}{m}$,$\\dfrac{\\pi m}{3qB}$;
"]]作出正电荷在磁场中运动的轨迹,如图所示
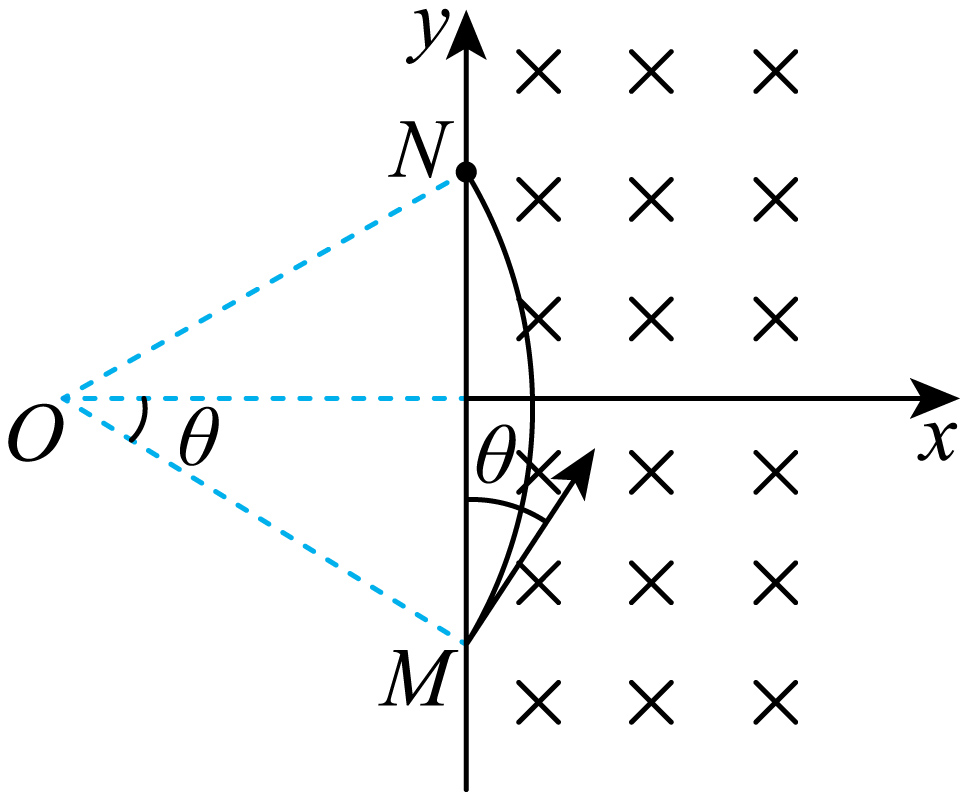
由几何关系可知,正电荷在磁场中做匀速圆周运动的半径为$r=\dfrac{y_{0}}{\sin\theta}=2y_{0}$
由洛伦兹力提供向心力$qv_{1}B=m\dfrac{v_{1}^{2}}{r}$
解得正电荷的入射速度大小为$v_{1}=\dfrac{2qBy_{0}}{m}$
正电荷在磁场中运动的周期为$T=\dfrac{2\pi r}{v_{1}}=\dfrac{2\pi m}{qB}$
所以正电荷从$M$运动到$N$的时间为$t_{1}=\dfrac{2\theta}{2\pi}T=\dfrac{\pi m}{3qB}$;
若在$xOy$平面内某点固定一负点电荷,电荷量为$48q$,粒子质量取$m= \dfrac{B^{2}y_{0}^{3}}{k}$($k$为静电力常量),粒子仍沿($1$)中的轨迹从$M$点运动到$N$点,求射入磁场的速度大小$v_{2}$;
$\\dfrac{6kq}{By_{0}^{2}}$;
"]]由题意可知,在$xOy$平面内的负电荷在圆心$O$处,由牛顿第二定律可知$qv_{2}B+k\dfrac{48q^{2}}{r^{2}}= m\dfrac{v_{2}^{2}}{r}$,其中$m= \dfrac{B^{2}{y_{0}}^{3}}{k}$
解得$v_{2}=\dfrac{6kq}{By_{0}^{2}}$或$v_{2}=\dfrac{- 4kq}{By_{0}^{2}}$(舍去);
在($2$)问条件下,粒子从$N$点射出磁场开始,经时间$t_{2}$速度方向首次与$N$点速度方向相反,求$t_{2}$(电荷量为$Q$的点电荷产生的电场中,取无限远处的电势为$0$时,与该点电荷距离为$r$处的电势$\varphi=\dfrac{kQ}{r}$)。
$\\dfrac{2\\sqrt{3}\\pi By_{0}^{3}}{3kq}$。
"]]在($2$)的条件下,正电荷从$N$点离开磁场后绕负电荷做椭圆运动,如图所示
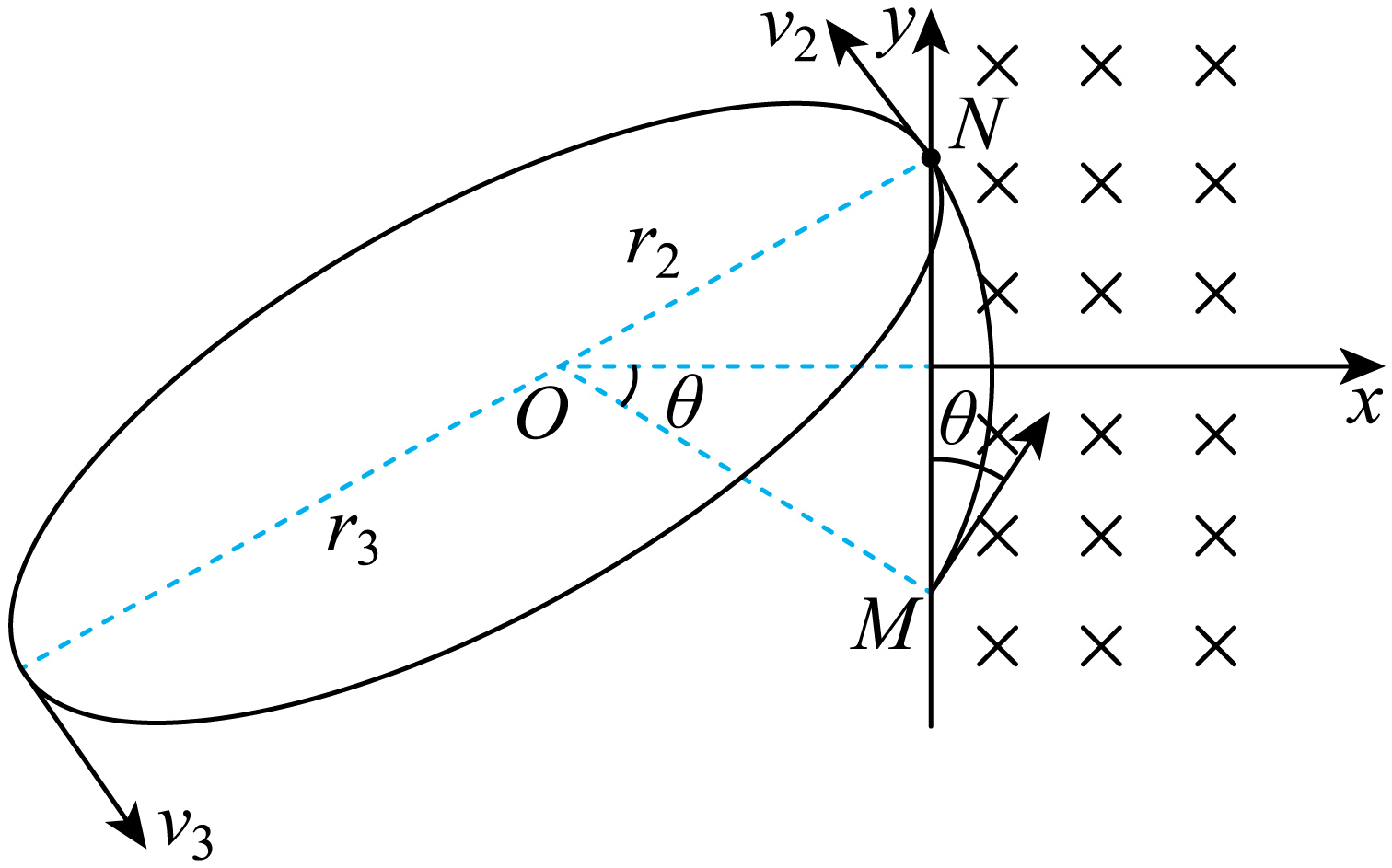
由能量守恒定律得$\dfrac{1}{2}mv_{2}^{2}-q\dfrac{k48q}{r_{2}}=\dfrac{1}{2}mv_{3}^{2}-q\dfrac{k48q}{r_{3}}$
由开普勒第二定律可知$v_{2}r_{2}=v_{3}r_{3}$
其中$r_{2}=2y_{0}$
联立解得$r_{3}=6y_{0}$
由牛顿第二定律$k\dfrac{48q^{2}}{{\left(\dfrac{r_{2}+r_{3}}{2}\right)}^{2}}=m\left(\dfrac{r_{2}+r_{3}}{2}\right)\dfrac{4\pi^{2}}{T^{2}}$
解得$T=\dfrac{4\sqrt{3}\pi By_{0}^{3}}{3kq}$
故正电荷从$N$点离开磁场后到首次速度变为与$N$点的射出速度相反的时间为$t_{2}=\dfrac{2\sqrt{3}\pi By_{0}^{3}}{3kq}$。
高中 | 牛顿第二定律的两类基本问题题目答案及解析(完整版)
