（$2024·$河南$·$二模）如图所示，一光滑的正三角形斜面体$OAB$放在光滑的水平地面上，不可伸长的轻绳两端分别栓接质量为$m_{1}$、$m_{2}$的两物体，轻绳跨过固定在$O$点的光滑滑轮，$m_{1}$、$m_{2}$分别放在$OA$、$OB$面上，两部分轻绳与斜面均平行。作用在斜面体上的恒力使斜面体向右做匀加速运动，$m_{1}$、$m_{2}$与斜面体保持相对静止，且$m_{1}$恰好没有离开斜面，则$m_{1}$、$m_{2}$的比值为$(\qquad)$

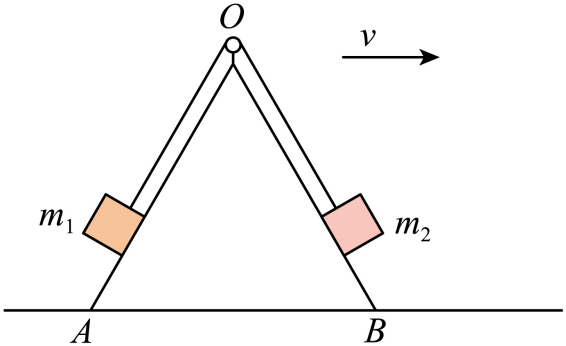
$1$∶$2$

$1$∶$1$

$3$∶$4$

$2$∶$1$

对$m_{1}$、$m_{2}$受力分析如图所示

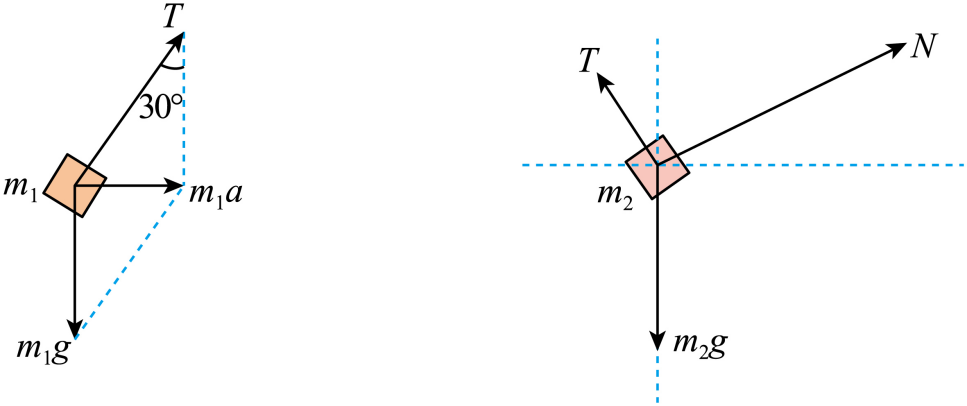
因为$m_{1}$恰好没有离开斜面，故其和斜面无弹力，可知绳上的弹力$T=\dfrac{2\sqrt{3}}{3}m_{1}g$

整体的加速度$a=\dfrac{\sqrt{3}}{3}g$

对$m_{2}$有$\dfrac{\sqrt{3}}{2}N-\dfrac{1}{2}T=m_{2}a$，$\dfrac{1}{2}N+\dfrac{\sqrt{3}}{2}T=m_{2}g$

两式联立解得$m_{1} : m_{2}=1 : 2$。

故选：$\rm A$。