| 动能定理解决多过程问题 题目答案及解析
稿件来源:高途
| 动能定理解决多过程问题题目答案及解析如下,仅供参考!
必修2
第七章 机械能守恒定律
7.7 动能和动能定理
动能定理解决多过程问题
如图所示,一个质量为$0.4\;\rm kg$的小球,以初速度$v_{0}$从$A$点平抛出去,恰好从$B$点沿切线进入圆弧,经过圆弧后从$D$点射出,又恰好落到$B$点。已知圆弧半径$R=2\;\rm m$,$\theta=60^\circ $,$A$与$D$高度差为$R=2\;\rm m$,$g=10\;\rm m/s^{2}$。求:
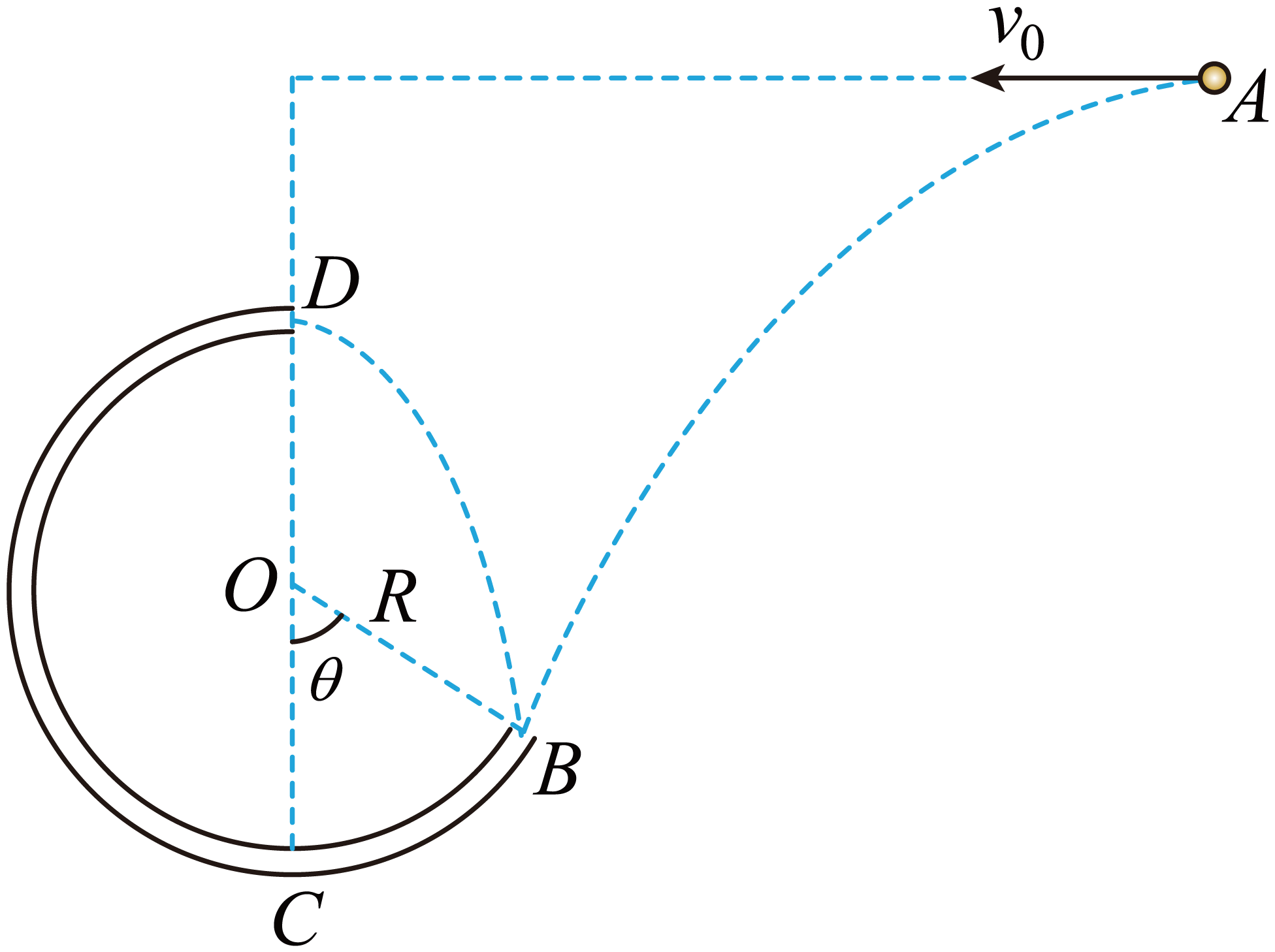
$v_{0}$的大小;
$v_{0}= \\dfrac{10\\sqrt{3}}{3}\\;\\text{m}/\\text{s}$;
"]]小球从$A$到$B$做平抛运动,竖直方向上有$R\left( 2+\cos\theta \right)=\dfrac{1}{2}gt^{2}$
解得$t=1\;\rm s$
到达$B$点时$\tan\theta=\dfrac{v_{y}}{v_{0}}=\dfrac{gt}{v_{0}}$
联立可得$v_{0}=\dfrac{10\sqrt{3}}{3}\ \text{m}/\text{s}$
$A$、$D$的水平距离;
$s= \\dfrac{13\\sqrt{3}}{3}\\text{ }\\text{m}$;
"]]$A$、$D$的水平距离为$s=v_{0}t+R\sin \theta$
解得$s=\dfrac{13\sqrt{3}}{3}\text{ }\text{m}$
在$D$点时,小球对管壁的作用力。
$-3 N$方向竖直向下
"]]小球从$D$到$B$:$R\sin \theta=v_{D}t_{1}$
$R\left( 1+\cos\theta \right)=\dfrac{1}{2}gt_{1}^{2}$
解得$v_{D}=\sqrt{5}\text{ }\text{m}/\text{s}$
在$D$点$mg-{F}'_{\text{N}}=m\dfrac{v_{D}^{2}}{R}$
解得$F'_{\rm N}=3\;\rm N$
小球对管壁的作用力$F_{\rm N}=−F'_{\rm N}=-3\;\rm N$
方向竖直向下。
| 动能定理解决多过程问题题目答案及解析(完整版)
