该同学在实验中得到如图$2$所示的一条纸带（相邻两计数点间还有四个点没有画出），已知打点计时器采用的是频率为$50\;\rm Hz$的交流电，根据纸带可求出小车的加速度为                 ${\text{m/s}^{2}}$（结果保留$3$位有效数字）；

相邻两计数点间时间间隔$T=0.02 \times 5\;\rm s=0.1\;\rm s$

$DF$间的距离$DF=10.00\;\rm cm-4.40\;\rm cm=5.60\;\rm cm$

$DF$间的距离$BD=4.40\;\rm cm-1.00\;\rm cm=3.40\;\rm cm$

由图可知开始一段位移和后面差距较大，舍掉开始一段位移$AB$，利用$BF$间位移求加速度得$a=\dfrac{DF-BD}{(2T)^{2}}=\dfrac{(5.60-3.40) \times 10^{- 2}}{(2 \times 0.1)^{2}}\;\rm \text{m/s}^{2}=0.550\;\rm \text{m/s}^{2}$；

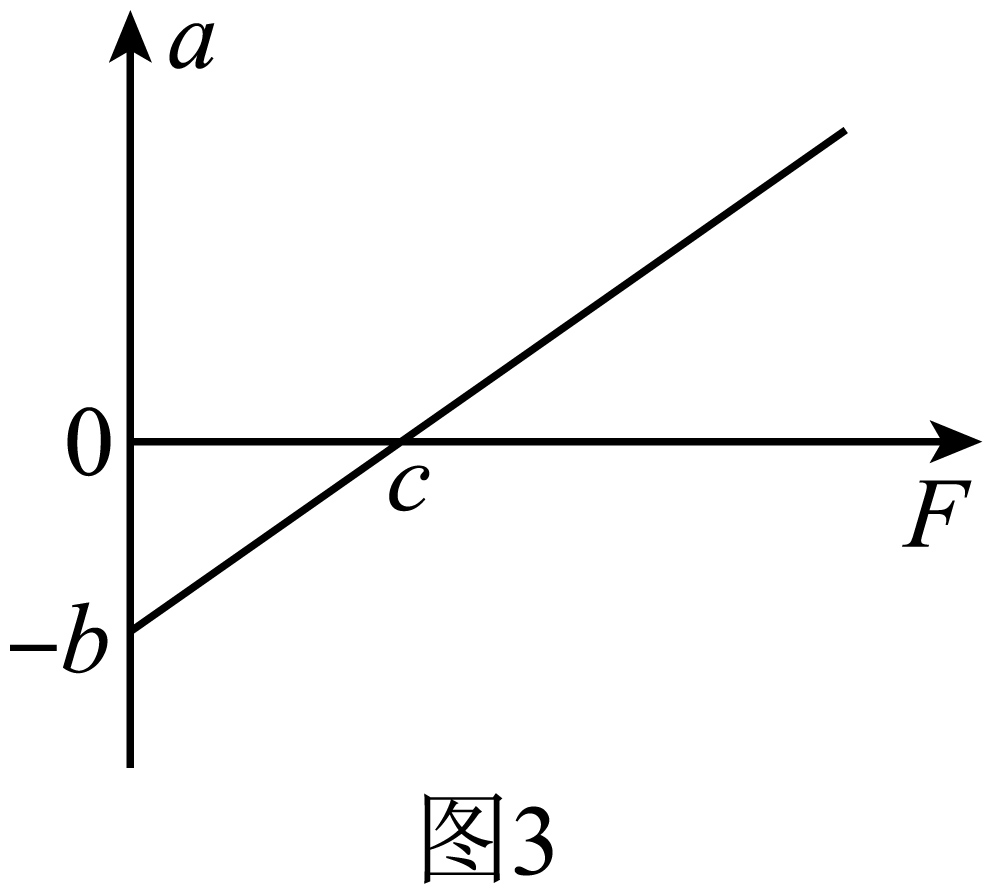
该同学以力传感器的示数$F$为横坐标，加速度$a$为纵坐标，画出的$a-F$图像是一条直线，如图$3$所示，则小车和车上的滑轮的总质量$M$为                 ；  

由牛顿第二定律得$2F − \mu Mg=Ma$

$a=\dfrac{2}{M}F-\mu g$

图线斜率$k=\dfrac{b}{c}=\dfrac{2}{M}$

得$M=\dfrac{2c}{b}$；

该实验                 （填“需要”或“不需要”）钩码的质量$m$远小于小车和车上滑轮的总质量$M$；

本实验绳子拉力可以由力传感器测出，不需要使小桶（包括沙）的质量远小于车的总质量；

小车和木板之间的动摩擦因数$\mu =$                 。

图线在纵轴的截距大小为$b=\mu g$

得$\mu=\dfrac{b}{g}$。