| 斜面问题 题目答案及解析
稿件来源:高途
| 斜面问题题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.6 用牛顿运动定律解决问题(一)
斜面问题
利用图甲所示带有位移传感器的装置可测量滑块与木板间的动摩擦因数$\mu $。将滑块从倾角为$\theta$的木板上由静止释放,位移传感器连接的计算机描绘出了滑块位移随时间的变化规律如图乙所示。(重力加速度$g=10\;\rm m/s^{2}$,$\sin 37^\circ =0.6$,$\cos 37^\circ =0.8$)
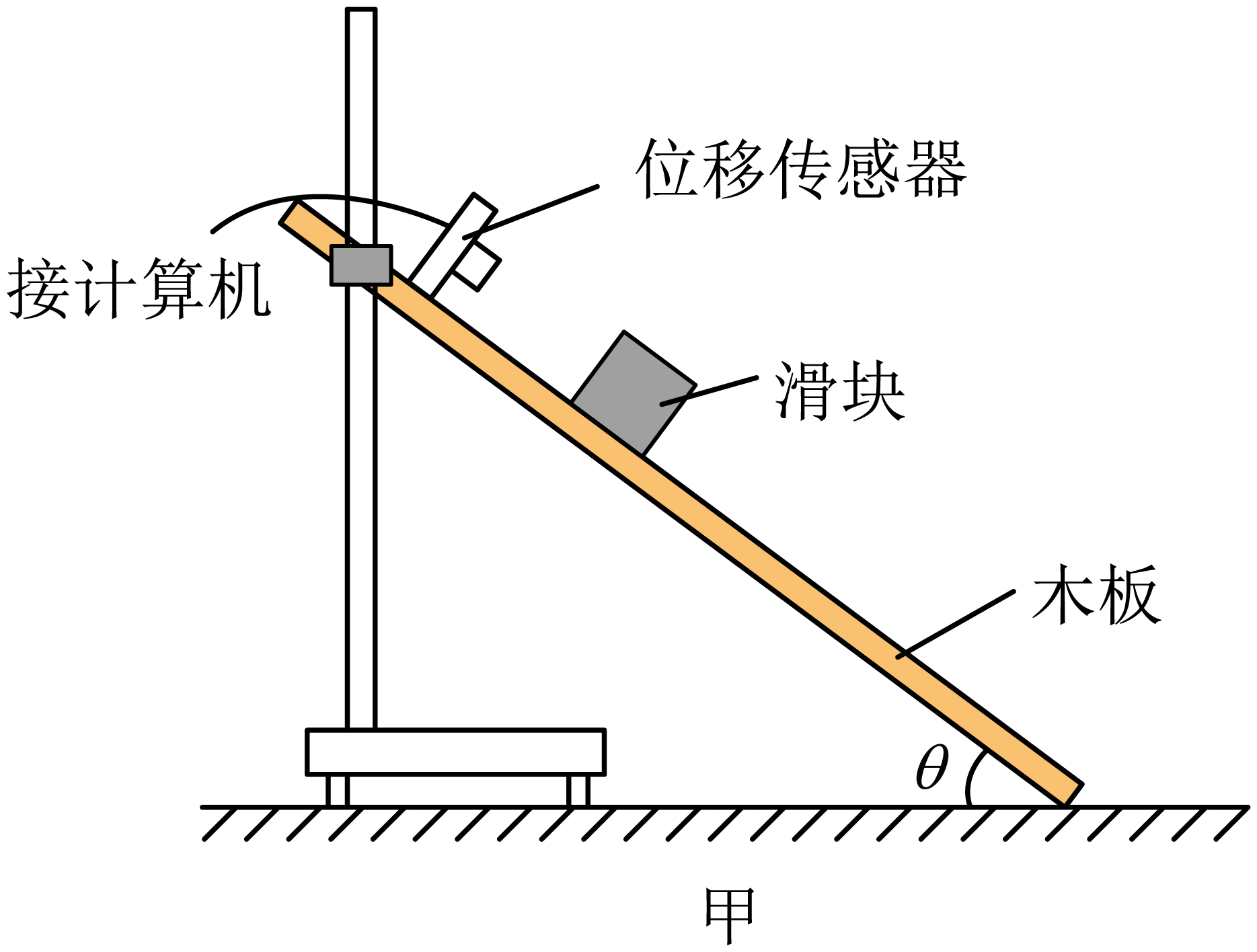
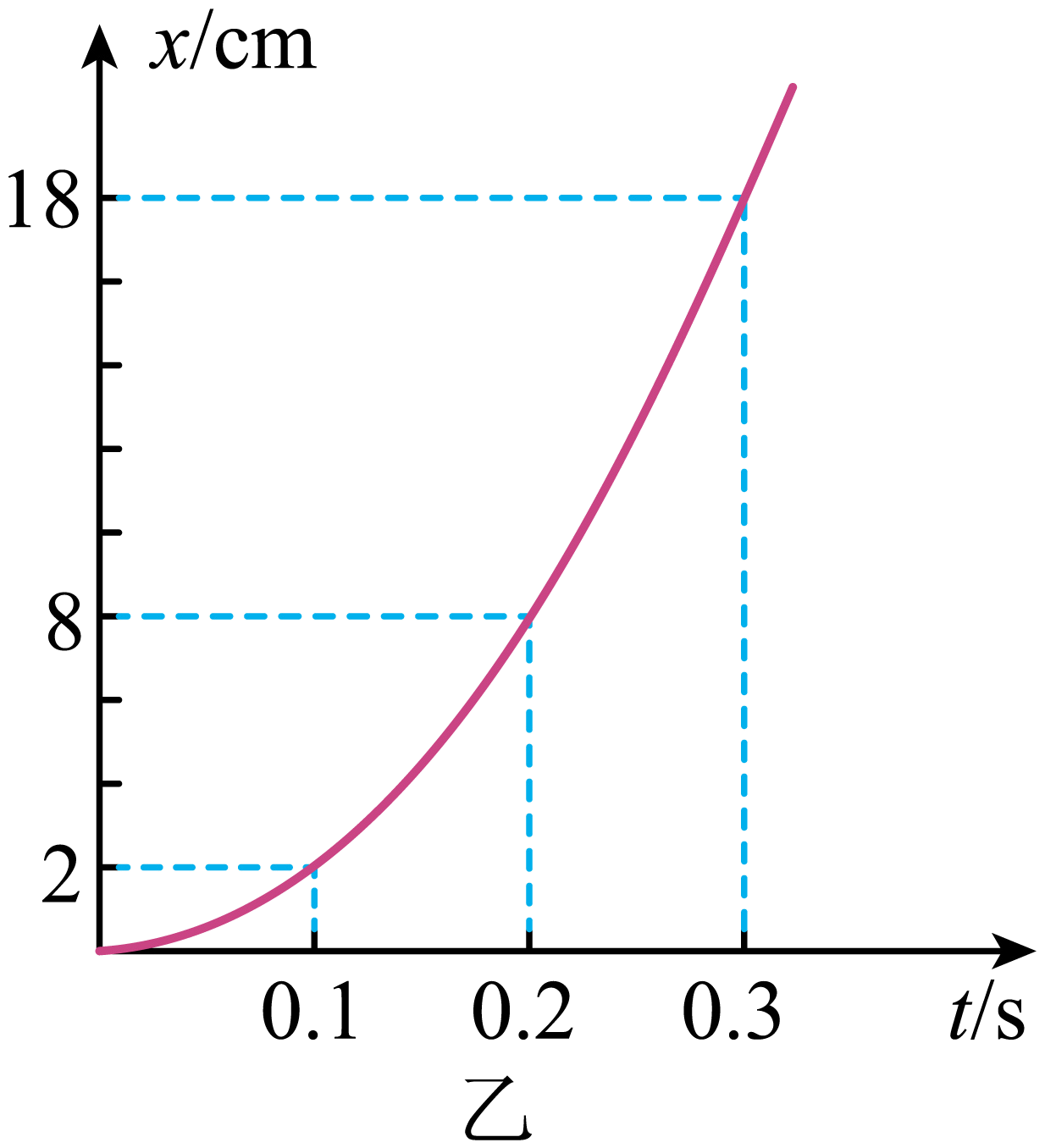
根据图乙数据可得滑块在$0.1\;\rm s$时的速度大小$v_{1}=$ $\;\rm m/s$;
根据匀变速直线运动中间时刻的瞬时速度等于这段时间内的平均速度可知滑块在$0.1\;\rm s$时的速度大小为$v_{1}=\dfrac{x}{t}=\dfrac{0.08}{0.2}\;\rm m/s=0.4\;\rm m/s$
滑块加速度大小$a=$ $\;\rm m/s^{2}$;
滑块在$0.2\;\rm s$时的速度大小为$v_{2}=\dfrac{x}{t}=\dfrac{0.16}{0.2}\;\rm m/s=0.8\;\rm m/s$
所以滑块的加速度为$a=\dfrac{v_{2}-v_{1}}{t}=4\;\rm m/s^{\text{2}}$
若测得斜面倾角为$\theta=37^\circ $,则动摩擦因数$\mu =$ 。
斜面倾角为$\theta=37^\circ $时,对滑块进行受力分析,根据牛顿第二定律得$ma=mg\sin \theta − \mu mg\cos \theta$
解得$\mu =0.25$
| 斜面问题题目答案及解析(完整版)
