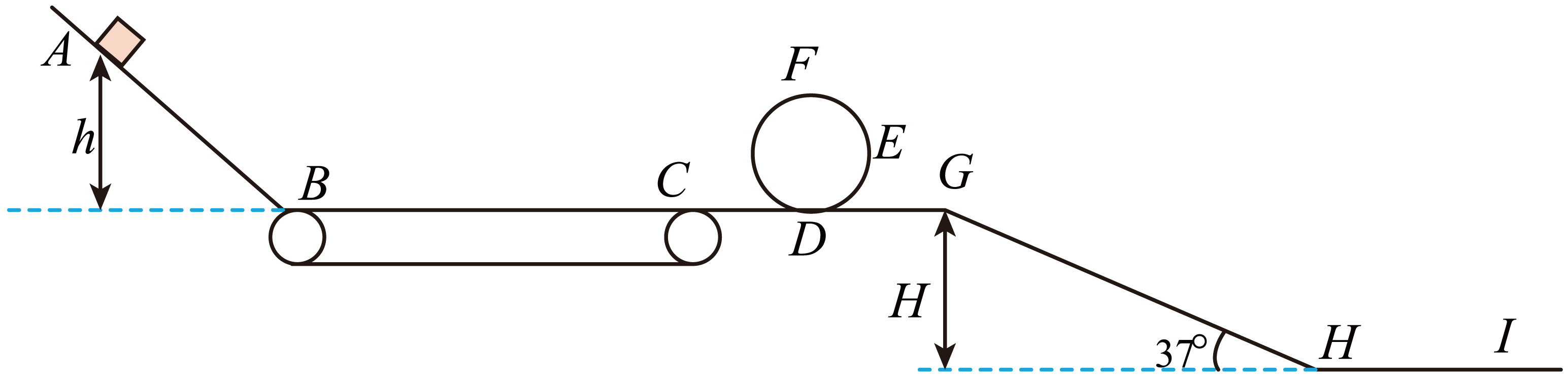
若小滑块质量为$0.1\;\rm kg$，释放的高度$h=1.2\;\rm m$，求小滑块通过$E$点时对轨道的压力；

$4\\;\\rm N$，方向水平向右

$A$到$E$，由动能定理得$mg(h-R)-\mu mgL=\dfrac{1}{2}mv_{E}^{2}- 0$

在$E$点，由牛顿第二定律得$F_{{N}}=\dfrac{mv_{E}^{2}}{R}$

联立得$F_{N}=4\ \rm N$

由牛顿第三定律得$F_{压}=F_{N}=4\ \rm N$，方向水平向右

为了使小滑块进入圆轨道且不脱离圆轨道$DEF$，求小滑块释放高度的范围；

见解析

滑块恰好到进入圆轨道，由动能定理得$mgh-\mu mgL=0-0$

解得$h=0.6\;\rm m$

使小滑块进入圆轨道，则$h\geqslant 0.6\;\rm m$

①滑块恰好到$E$点，由动能定理得$mg(h-R)-\mu mgL=0-0$

解得$h=0.8\;\rm m$

使小滑块进入圆轨道且不脱离圆轨道，则$0.6\;{\rm m}\leqslant h\leqslant 0.8\;\rm m$

②滑块恰好到$F$点，由动能定理得$mg(h-2R)-\mu mgL=\dfrac{1}{2}mv_{F}^{2}-0$

在$F$点，由牛顿第二定律得$mg=\dfrac{mv_{F}^{2}}{R}$

解得$h=1.1\;\rm m$

要使小滑块进入圆轨道且不脱离圆轨道，则$h\geqslant 1.1\;\rm m$

若小滑块释放的高度$h=0.65\;\rm m$，同时调节传送带以不同速度顺时针转动，为了保证小滑块不脱离圆轨道又能从$G$点水平飞出，试写出小滑块第$1$次落点（不反弹）与$G$点的水平距离$x$与传送带速度$v$的关系。

见解析

由题意可知，滑块过最高点$F$，则$C$到$F$，由动能定理得$- mg \cdot 2R=\dfrac{1}{2}mv_{E}^{2}- \dfrac{1}{2}mv_{C}^{2}$

联立得$v_{C}=\sqrt{10}\;\text{m}/\text{s}$

即滑块过最高点$F$，必须满足$v_{C} \geqslant \sqrt{10}\;\text{m}/\text{s}$

滑块从$G$点水平飞出，恰好落在$H$点。则$H=\dfrac{1}{2}gt^{2}$，$x=vt$

解得：$t=0.6\;\rm s$，$v=4\;\rm m/s$

①当$\sqrt{10}\;\text{m}/\text{s} \leqslant v \lt 4\;\text{m}/\text{s}$时，落点均在斜面上，则$\tan37{^\circ}=\dfrac{y}{x}=\dfrac{\dfrac{1}{2}gt^{2}}{vt}=\dfrac{gt}{2v}$

解得$t=\dfrac{2v\tan37{^\circ}}{g}\text{ }x=vt=\dfrac{3v^{2}}{2g}$

②当$4\;{\rm m/s}\leqslant v\leqslant 5\;\rm m/s$时，$x=0.6v(\rm m)$

③当$v\gt5\;\rm m/s$时，$x=3\;\rm m$