高中 | 闭合电路的欧姆定律基本问题 题目答案及解析
稿件来源:高途
高中 | 闭合电路的欧姆定律基本问题题目答案及解析如下,仅供参考!
选修3-1
第二章 恒定电流
2.7 闭合电路的欧姆定律
闭合电路的欧姆定律基本问题
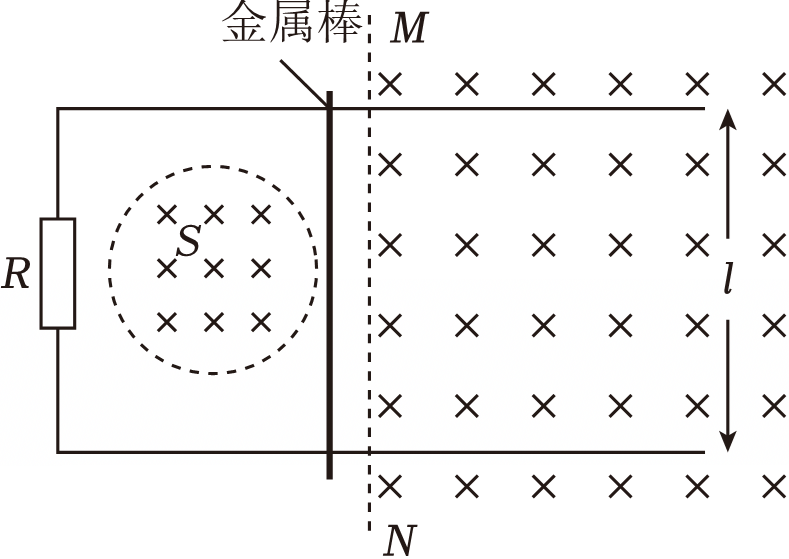
如图,两条相距$l$、电阻不计的光滑平行金属导轨位于水平面(纸面)内,其左端接一阻值为$R$的电阻。一金属棒垂直置于两导轨上,接入电路部分的电阻为$r$;在导轨和金属棒中间有一面积为$S$的区域,区域中存在垂直于纸面向里的均匀磁场,磁感应强度大小$B$随时间$t$的变化关系为$B_{0}=kt(k\gt 0)$,式中$k$为常量;在金属棒右侧有一匀强磁场,左边界$MN$(虚线)与导轨垂直,磁感应强度大小为$B_{1}$,方向垂直于纸面向里。某时刻,金属棒在一外加水平恒力的作用下从静止开始向右运动,在$t_{0}$时刻恰好以速度$v_{0}$越过$MN$,此后向右做匀速运动,金属棒与导轨始终相互垂直并接触良好。求:
$0-t_{0}$内,通过电阻$R$的电荷量$q$;
$0-t_{0}$内,通过电阻$R$的电荷量$q$为$\\frac{k{t}_{0}S}{R+r}$;
"]]$0-t_{0}$内,根据法拉第电磁感应定律有:${E}_{0}=\frac{\triangle {B}_{0}S}{\triangle t}=kS$
回路中感应电流为:$I=\frac{{E}_{0}}{R+r}=\frac{kS}{R+r}$
又因为:$q=It_{0}$
所以:$q=\frac{k{t}_{0}S}{R+r}$
$0-t_{0}$内,电阻$R$的发热量$Q$;
$0-t_{0}$内,电阻$R$的发热量$Q$为$\\frac{{k}^{2}{S}^{2}R{t}_{0}}{{(R+r)}^{2}}$;
"]]由于该时间内电流恒定,所以根据焦耳定律得热量:$Q=I^{2}Rt_{0}$
代入数据可得:$Q=\frac{{k}^{2}{S}^{2}R{t}_{0}}{{(R+r)}^{2}}$
金属棒所受水平恒力$F$的大小。
金属棒所受水平恒力$F$的大小为$\\frac{{B}_{1}(kS+{B}_{1}l{v}_{0})l}{R+r}$。
"]]导体棒切割磁感线,动生电动势:$E_{1}=B_{1}lv_{0}$
感生电流和动生电流同时存在且方向相同,所以总电动势:$E=E_{0}+E_{1}$
感应电流大小:$I=\frac{E}{R+r}$
安培力大小:${{F}_{}}={{B}_{1}}Il$
金属棒匀速则:$F={{F}_{}}$
联立代入数据可得:$F=\frac{{B}_{1}(kS+{B}_{1}l{v}_{0})l}{R+r}$
高中 | 闭合电路的欧姆定律基本问题题目答案及解析(完整版)
