一根轻质弹性绳的两端分别固定在水平天花板上相距$60\;\rm cm$的两点上，弹性绳的原长也为$60\;\rm cm$；将一钩码挂在弹性绳的中点，平衡时弹性绳的总长度为$100\;\rm cm$；再将弹性绳的两端缓慢移至天花板上的同一点，则弹性绳的总长度变为（弹性绳的伸长始终处于弹性限度内）$(\qquad)$

$76\\;\\rm cm$

$82\\;\\rm cm$

$86\\;\\rm cm$

$92\\;\\rm cm$

由题意可得如图所示

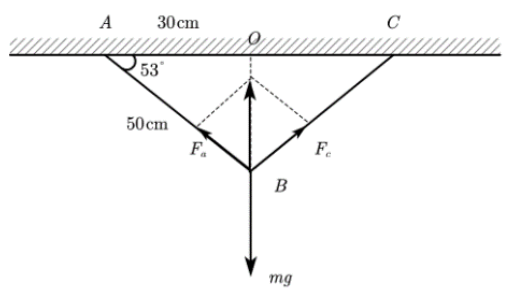
假设每段绳子的劲度系数为$k$，则绳子拉力为$F=0.2k$

把绳子的拉力分解为水平方向和竖直方向，在竖直方向的分量为$F_{y}=0.2k \times \sin53^\circ =0.16k$

两个绳子的竖直方向拉力合力为$2F_{y}$，由平衡可得$0.32k=mg$

解得$k=\dfrac{mg}{0.32}$

当$AC$两点移动到同一点时，绳子两个绳子的夹角为$0$，每段绳子伸长$x'$，则两个绳子的拉力合力为$2kx'=mg$

得$x'=0.16\;\rm m$

所以此时绳子总长度为$92\;\rm cm$。

故选：$\rm D$。