德国天文学家开普勒研究发现行星的运动具有相似性，并将其总结为开普勒行星运动定律。牛顿认为天体运动和地面物体运动规律相似，在开普勒行星运动定律的基础上，推演得到了万有引力定律。

①理论和实践证明，开普勒定律不仅适用于太阳系中的天体运动，而且适用于一切天体运动。若研究地球的卫星运动，开普勒第三定律公式$\dfrac{a^{3}}{T^{2}}=k$中的$k$与什么有关系$(\qquad)$

$\rm A$．卫星质量      $\rm B$．地球质量      $\rm C$．太阳质量

②（论述）请论述据开普勒定律和牛顿定律得到万有引力定律的过程                 ；

根据开普勒第三定律可知$\dfrac{a^{3}}{T^{2}}= k$，其中$k$与行星或卫星无关，只与中心天体有关，因此在研究地球的卫星运动时，$k$只与地球的质量有关；

故选：$\rm B$；

设行星的质量为$m$，行星的线速度为$v$，行星与太阳之间的距离为$r$，太阳对行星的万有引力为$F$，根据圆周运动规律则有$F=m\dfrac{v^{2}}{r}$

天文观测可得行星得公转周期$T$，则由此可得行星的线速度$v=\dfrac{2\pi r}{T}$

联立可得$F=\dfrac{4\pi^{2}mr}{T^{2}}$

根据开普勒第三定律可知$\dfrac{r^{3}}{T^{2}}=k$

整理可得$F=4\pi^{2}k\dfrac{m}{r^{2}}$

即$F \propto \dfrac{m}{r^{2}}$

根据牛顿第三定律可知，行星对太阳的引力也应与太阳的质量成正比，即$F \propto \dfrac{m_{太}}{r^{2}}$

由于$F \propto \dfrac{m}{r^{2}}$，$F \propto \dfrac{m_{太}}{r^{2}}$

可得$F \propto \dfrac{mm_{太}}{r^{2}}$

写成等式为$F=G\dfrac{m_{1}m_{2}}{r^{2}}$；

静电场和引力场有许多相似之处。类比电场强度和电势的定义，已知引力常量为$G$，质量为$M$的质点产生的引力场中，与之相距$r$的地方引力场强度$E_{G}=$                 ；引力势$\varphi_{G}=$                 ；（以无穷远处为零势能面）

类比电场强度可知，引力强度为$E_{G} =\dfrac{F_{引}}{m}=\dfrac{\dfrac{GMm}{r^{2}}}{m}= \dfrac{GM}{r^{2}}$

引力势应等于引力势能与质量的比值，即$\varphi_{G}=\dfrac{E_{\rm{p}引}}{m}=\dfrac{- \dfrac{GMm}{r}}{m}=- \dfrac{GM}{r}$；

原子的核式结构模型有些类似太阳系，原子核犹如太阳，电子犹如行星，所以也被称为原子的“行星模型”。

①类比太阳系，以无穷远处为零势能面，氢原子中电子与氢原子核间静电相互作用的电势能为$（k$为静电力常量，$r$为电子轨道半径）             

$\rm A$．$k\dfrac{e^{2}}{r}$      $\rm B$．$- k\dfrac{e^{2}}{r}$      $\rm C$．$k\dfrac{e^{2}}{r^{2}}$      $\rm D$．$- k\dfrac{e^{2}}{r^{2}}$

②氢原子的核外电子吸收电磁波从一个轨道跃迁至另一轨道，关于电子绕核运动的动能，原子的电势能，以及动能和电势能的总和说法正确的是$(\qquad)$

$\rm A$．动能增大，电势能减小，总和不变

$\rm B$．动能减小，电势能增大，总和不变

$\rm C$．动能减小，电势能增大，总和增大

电子与氢原子核之间的静电力$F= k\dfrac{e^{2}}{r}$

类比引力势能可知，氢原子中电子与氢原子核间静电相互作用的电势能为$E_{\rm {p}电}=- \dfrac{ke^{2}}{r}$

故选：$\rm B$；

根据玻尔理论，原子吸收光子后，原子的总能量增大，核外电子从距核较近的轨道跃迁到距核较远的轨道，核外电子做圆周运动的向心力由库仑力提供，电子与原子核的距离变大，库仑力减小，电子圆周运动的速度减小，动能减小，跃迁到较远的轨道时，库仑力做负功，电势能增大；

故选：$\rm C$；

如图为氢原子在可见光区的四条谱线$H_{\alpha}$、$H_{\beta}$、$H_{\gamma}$、$H_{\delta}$。对于四条谱线，下列说法中正确的是$(\qquad)$

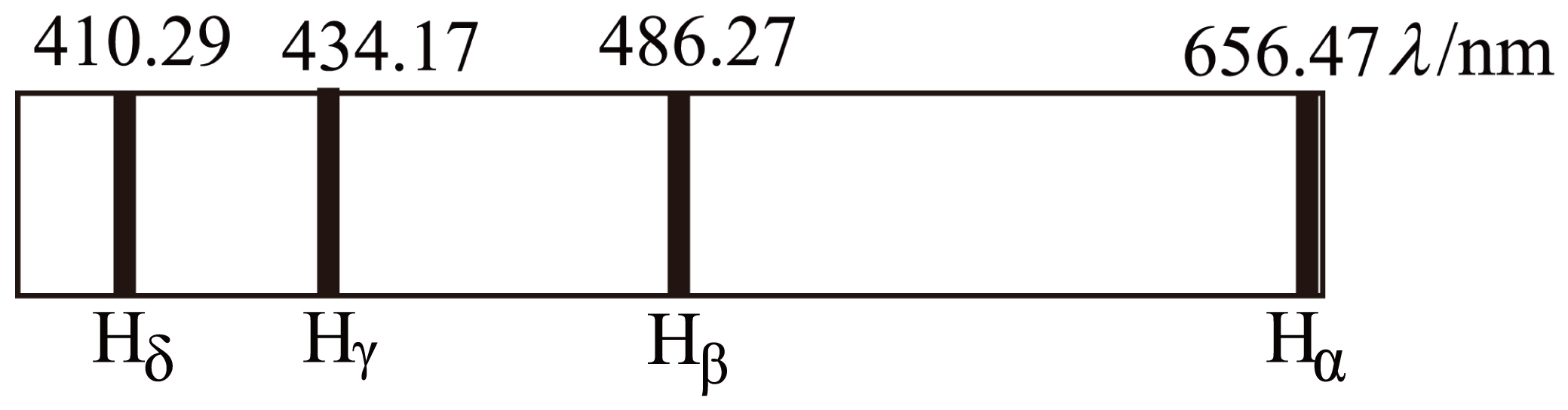
在同一介质中，$H_{\\alpha}$的速度最大

由同一介质射入空气，$H_{\\alpha}$的临界角最小

$H_{\\alpha}$更容易发生衍射现象

$H_{\\alpha}$对应的光子动量最小

$\rm A$．由图可知，$H_{\alpha}$的波长最长，频率最小，折射率最小，根据$v=\dfrac{c}{n}$可知，在同一种介质中，$H_{\alpha}$的速度最大，$\rm A$正确；

$\rm B$．由于$H_{\alpha}$折射率最小，根据$\sin C=\dfrac{1}{n}$可知，由同一种介质进入空气，$H_{\alpha}$临界角最大，$\rm B$错误；

$\rm C$．由于$H_{\alpha}$波长最长，更容易发生衍射现象，$\rm C$正确；

$\rm D$．根据$p=\dfrac{h}{\lambda}$可知，$H_{\alpha}$的波长最长，其对应光子的动量最小，$\rm D$正确；

故选：$\rm ACD$；

为解释氢原子光谱，玻尔在“行星模型”的基础上，引入量子化的概念，认为原子只能处于不连续的轨道和能量状态中。已知氢原子核外电子第$1$条（量子数$\lambda=1$）轨道半径$r_{1}=5.3 \times 10^{-11}\;\rm m$，普朗克常量$h=6.626 \times 10^{-34}\;\rm J ⋅ s$，求它从量子数$n=2$的激发态跃迁到基态，向外辐射的电磁波的波长。（结果保留$3$位有效数字）

$122\\;\\rm nm$。

对核外电子，根据牛顿第二定律则有$k\dfrac{e^{2}}{r^{2}}=\dfrac{mv^{2}}{r}$

结合动能公式可得，电子的动能$E_{\rm{k}}=\dfrac{1}{2}mv^{2}=\dfrac{ke^{2}}{2r}$

类比引力势能可得电子的势能$E_{\rm{p}}=- \dfrac{ke^{2}}{r}$

故电子的能量为$E=E_{\rm{k}}+E_{\rm{p}}=- \dfrac{ke^{2}}{2r}$

则氢原子核外量子数为$n=1$的电子的能量为$E_{1}=- \dfrac{ke^{2}}{2r_{1}}=- 9 \times 10^{9} \times \dfrac{{(1.6 \times 10^{- 19})}^{2}}{2 \times 5.3 \times 10^{- 11}}=- 2.17 \times 10^{- 18}\;\rm{J=}-13.6\;\rm {eV}$

氢原子核外量子数为$n$时的电子的能量为$E_{n}=\dfrac{1}{n^{2}}E_{1}$

故量子数为$n=2$电子的能量$E_{2}=\dfrac{1}{2^{2}}E_{1}=- 3.4\;\rm{eV}$

根据玻尔理论则有$h\dfrac{c}{\lambda}=E_{2}-E_{1}$

代入数据解得$\lambda=122\;\rm nm$。