用这四种光照射同一单缝衍射装置，中央明条纹宽度最宽的是$(\quad\ \ \ \ )$。

$H_{\\alpha}$光

$H_{\\beta}$光

$H_{\\gamma}$光

$H_{\\delta}$光

由于$H_{\delta}$光的波长最大，所以用这四种光照射同一单缝衍射装置，中央明条纹宽度最$H_{\delta}$光。

故选：$\rm D$。

用$H_{\beta}$光进行双缝干涉实验，在屏上观察到的干涉条纹如图甲所示，改变双缝间的距离后，干涉条纹如图乙所示，图中虚线是亮纹中心的位置。则双缝间的距离变为原来的$(\quad\ \ \ \ )$。

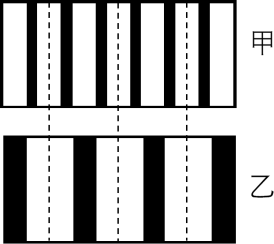
$\\dfrac{1}{3}$倍

$\\dfrac{1}{2}$倍

$2$倍

$3$倍

由题图可知，改变双缝间的距离后，根据相邻亮条纹间距变为原来的$2$倍；根据相邻亮条纹间距公式$\Delta x= \dfrac{L}{d}\lambda$可知，双缝间的距离变为原来的$\dfrac{1}{2}$倍。

故选：$\rm B$。

如图，将一束$H_{\gamma}$光沿半径方向从真空射向半圆形玻璃砖的表面，在圆心$O$处发生折射，虚线为过$O$的法线。

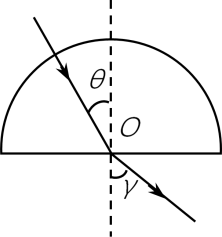
①若入射光与法线的夹角为$\theta$，折射光线与法线的夹角为$\gamma$，则玻璃砖的折射率$n=$                 。

②增大$H_{\gamma}$光的入射角，折射光的强度将                 。

$\rm A$．增强          $\rm B$．减弱          $\rm C$．不变

①根据折射定律可得玻璃砖的折射率为$n= \dfrac{\sin\gamma}{\sin\theta}$

②增大$H_{\gamma}$光的入射角，则反射光的强度增大，折射光的强度将减弱。

故选：$\rm B$。