高中 | LC电磁振荡 题目答案及解析
稿件来源:高途
高中 | LC电磁振荡题目答案及解析如下,仅供参考!
选修3-4
第十四章 电磁波
14.2 电磁振荡
LC电磁振荡
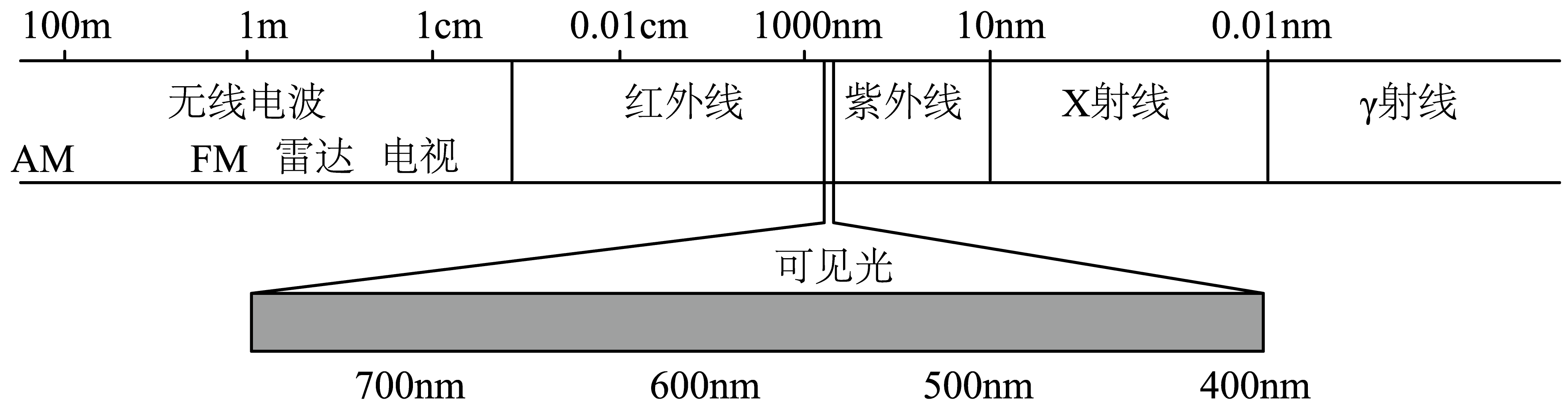
不同波长的电磁波有不同的应用,其产生机理也各不相同。把各类电磁波按波长大小排成一列,称为电磁波谱,如图所示。
$LC$振荡电路可产生无线电波。将一铜环放置在线圈上方,铜环平面与线圈中心轴线垂直,如图($a$)所示。电容器极板上的电荷量$q$随时间$t$变化的图线如图($b$)所示,则$(\qquad)$
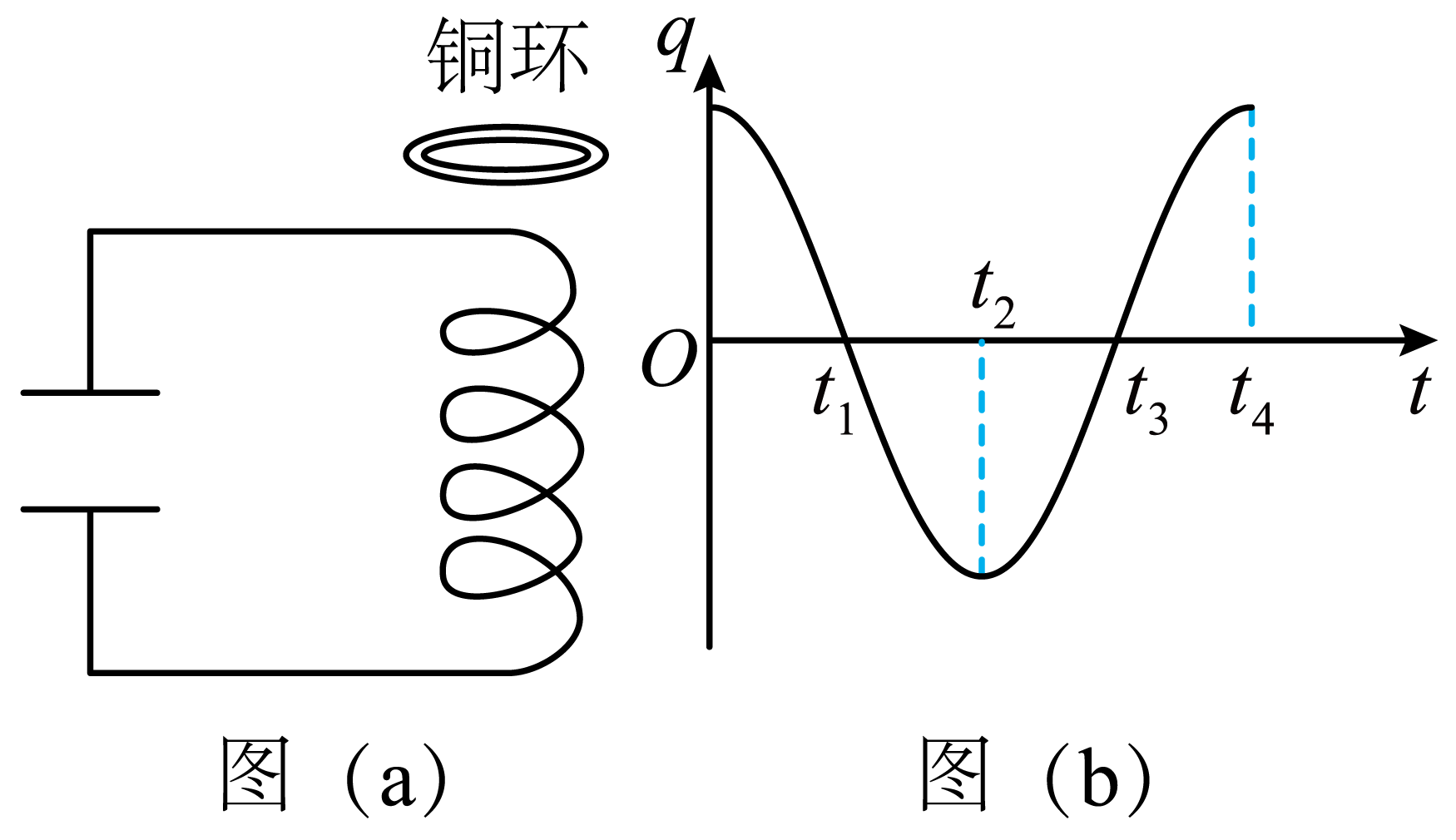
$t_{1}$、$t_{3}$时刻电路中电流最小
","$t_{2}$、$t_{4}$时刻电容器里电场最强
","$t_{1} ∼ t_{2}$时间内线圈和铜环相互排斥
","$t_{2} ∼ t_{4}$时间内电路中的电流方向不变
"]$\rm A$.在$LC$振荡电路中,电流与电荷量的变化率成正比。当电荷量达到最小值时,电流最大。因此,$t_{1}$、$t_{3}$时刻电容器电量最小,电路中的电流最大,$\rm A$错误;
$\rm B$.$t_{2}$、$t_{4}$时刻电容器电量最大,由$U=\dfrac{q}{C}$可知电容器里电场最强,$\rm B$正确;
$\rm C$.在$t_{1} ∼ t_{2}$时间内,电荷量从最小值增加到最大值,电流从最大值减小到零,线圈中磁场减弱,根据楞次定律,铜环中会产生感应电流,方向与线圈电流相同,导致线圈和铜环相互吸引,$\rm C$错误;
$\rm D$.$q − t$图像斜率表示电流,$t_{2} ∼ t_{3}$时间内电容器下极板带正电先放电,放电电流逆时针方向,$t_{3} ∼ t_{4}$时间内上极板带正电,电容器充电,电路中的电流方向逆时针,故$t_{2} ∼ t_{4}$时间内电路中的电流方向不变,$\rm D$正确;
故选:$\rm BD$;
如图所示为氢原子的能级图,已知氢原子从$n=4$的激发态直接跃迁到$n=2$的能级时发出蓝光。普朗克常量$h=6.63 \times 10^{-34}\;\rm J ⋅ s$。
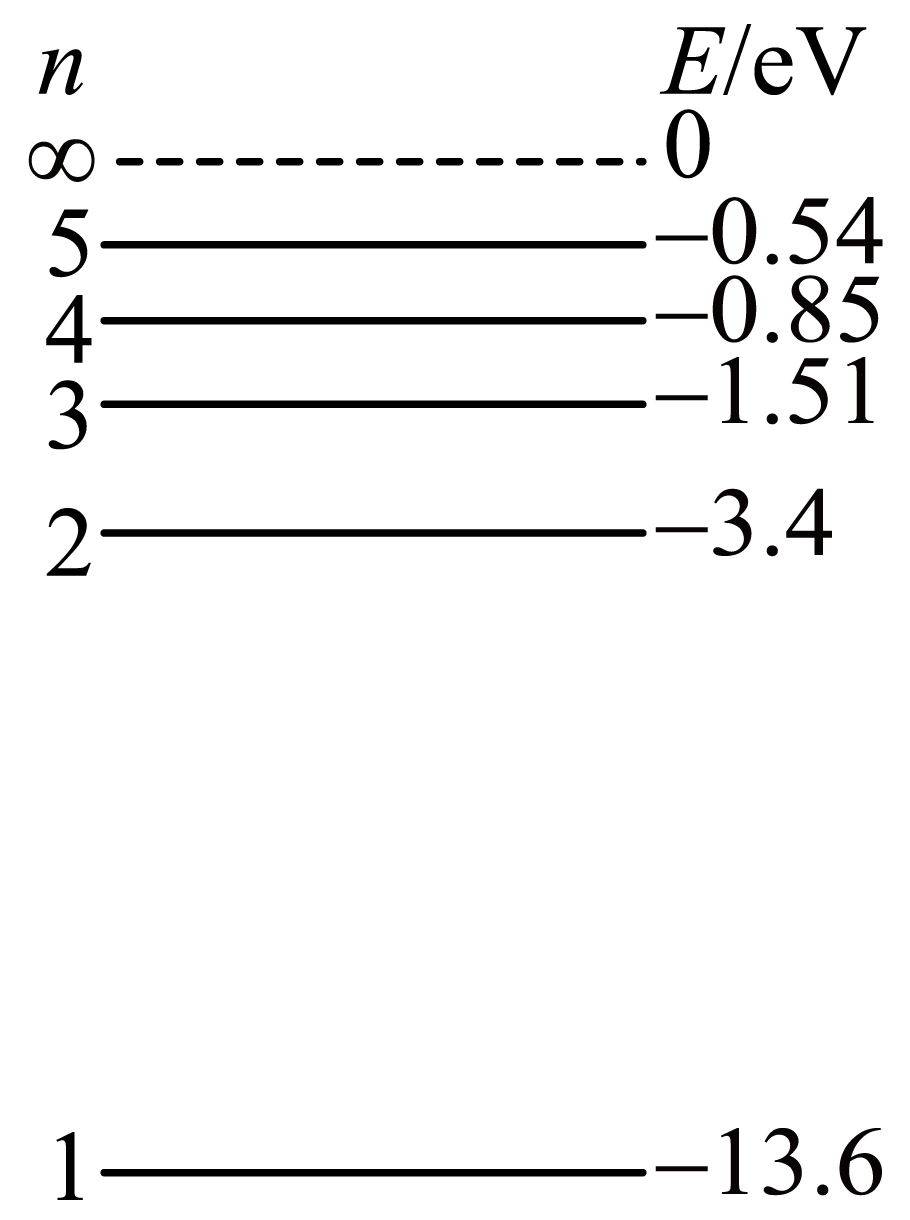
①氢原子从$n=3$的激发态直接跃迁到$n=2$的能级时可能发出 ;
$\rm A$.红外线 $\rm B$.红光 $\rm C$.紫光 $\rm D$.紫外线
②对上述($1$)中的选择做出解释 ;
已知氢原子从$n=4$的激发态直接跃迁到$n=2$的能级时发出蓝光。氢原子从$n=3$跃迁到$n=2$的能级差小于从$n=4$跃迁到$n=2$的能级差,因此发出的光子能量较低,波长较长,且为可见光,蓝光的波长较短,红光波长较长,故可能发出红光;
故选:$\rm B$;
氢原子从$n=3$跃迁到$n=2$的能级差小于从$n=4$跃迁到$n=2$的能级差,因此发出的光子能量较低,波长较长,且为可见光,蓝光的波长较短,红光波长较长,故可能发出红光;
一个中子与某原子核$\rm_{Z}^{A}X$结合成一个氘核($\rm _{1}^{2}H$)并放出能量为$E$的$\gamma$光子。
①该原子核中$A=$ ,$Z=$ 。
②已知中子质量为$m_{n}$,质子质量为$m_{\rm p}$,真空中的光速为$c$,则氘核的平均结合能为 。
核反应方程为$\rm _{0}^{1}n+_{Z}^{A}X→_{1}^{2}H$
由质量数守恒、电荷数守恒有$1+A=2$,$0+Z=1$
解得$A=1$,$Z=1$
由上述分析可知$\rm_{Z}^{A}X$为质子,已知中子质量为$m_{n}$,质子质量为$m_\rm{p}$,真空中的光速为$c$,则氘核的结合能为$(m_{\rm p}+m_{n})c^{2} − E$
氘核的平均结合能为$\dfrac{\left( m_{\rm{p}}+m_{{n}} \right)c^{2}-E}{2}$。
高中 | LC电磁振荡题目答案及解析(完整版)
