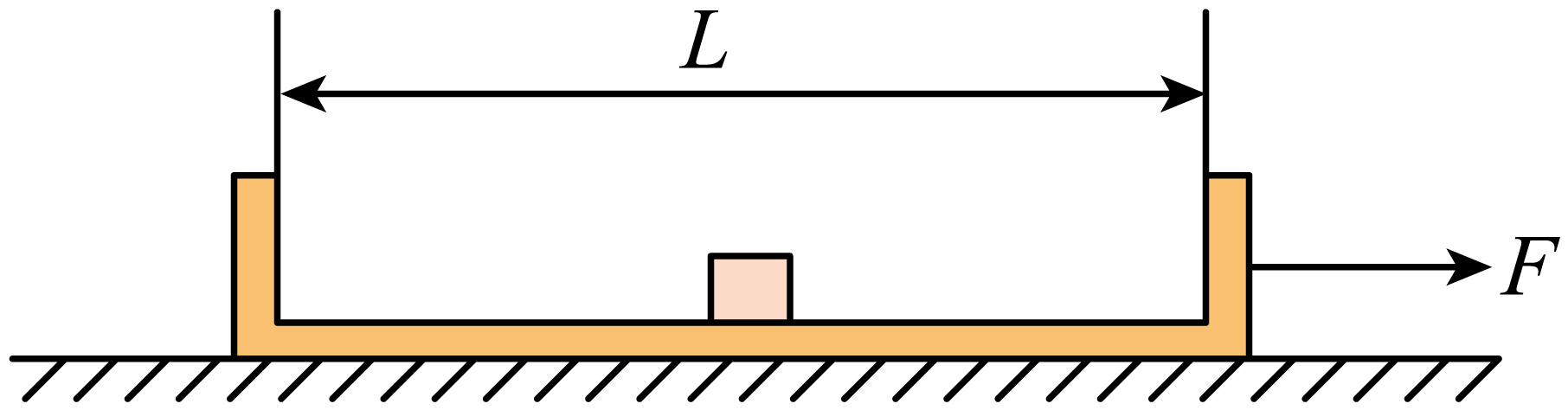
若给箱子施加向右的恒定外力$F$，要使物块与箱子不发生相对运动，则所施加外力的最大值为多少；

$F=30\\;\\rm N$

取物块为研究对象，根据牛顿第二定律可得$\mu mg=ma_{1}$

解得$a_{1}=2.5\;\rm m/s^{2}$

要使物块相对箱子不发生相对运动，则箱子的最大加速度为$2.5\;\rm m/s^{2}$，取整体为研究对象，根据牛顿第二定律可得$F=(M+m)a_{1}=30\;\rm N$

若给箱子施加$F=35\;\rm N$的外力，求物块经过多长时间与箱子的挡板相碰；

$t=4\\;\\rm s$

由于$F=35\;\rm N\gt30\;\rm N$

物块相对箱子发生相对运动，物块的加速度为$a_{1}=2.5\;\rm m/s^{2}$

取箱子为研究对象，根据牛顿第二定律可得$F-\mu mg=Ma_{2}$

解得$a_{2}=3\;\rm m/s^{2}$

物块向右做匀加速直线运动，相对于箱子向左运动，设物块运动到左侧的时间为$t$，则$\dfrac{1}{2}a_{2}t^{2}-\dfrac{1}{2}a_{1}t^{2}=\dfrac{L}{2}$

代入数据解得$t=4\;\rm s$

若给箱子施加$F=35\;\rm N$的外力$3\;\rm s$后，撤掉外力，求再经过多长时间，物块与箱子达到共速。

$t'=0.5\\;\\rm s$

由（$2$）知，当施加给箱子$35\;\rm N$的外力时，物块向右做$a_{1}=2.5\;\rm m/s^{2}$

的匀加速直线运动，箱子向右做$a_{2}=3\;\rm m/s^{2}$

的匀加速直线运动，撤掉外力$F$时，物块的速度$v_{1}=a_{1}t_{1}=7.5\;\rm m/s$

箱子的速度$v_{2}=a_{2}t_{1}=9\;\rm m/s$

箱子的速度$v_{2}\gt v_{1}$，物块继续以$2.5\;\rm m/s^{2}$的加速度加速，分析箱子的受力，根据牛顿第二定律可得$\mu mg=Ma_{3}$

解得$a_{3}=0.5\;\rm m/s^{2}$

箱子向右做加速度大小为$0.5\;\rm m/s^{2}$的匀减速直线运动，设经历时间$t'$二者共速，根据运动学公式可得$v_{1}+a_{1}t'=v_{2}-a_{3}t'$

解得$t'=0.5\;\rm s$