| 牛顿第二定律的两类基本问题 题目答案及解析
稿件来源:高途
| 牛顿第二定律的两类基本问题题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.6 用牛顿运动定律解决问题(一)
牛顿第二定律的两类基本问题
如图甲所示,倾角为$\theta=37^\circ $的足够长的光滑斜面体放置在光滑水平面上,上端有垂直斜面的挡板,与斜面平行的轻弹簧上端固定在挡板上,下端连接质量为$m=1\;\rm kg$的物块(可视为质点)。现对斜面体施加一水平向右的推力$F$,测得推力$F$的大小随弹簧的形变量$x$的变化规律如图乙所示(取弹簧伸长为正,压缩为负)。若弹簧始终在弹性限度内,重力加速度$g=10\;\rm m/s^{2}$,$\sin37^\circ =0.6$,$\cos37^\circ =0.8$,则斜面体的质量和轻弹簧的劲度系数分别为$(\qquad)$
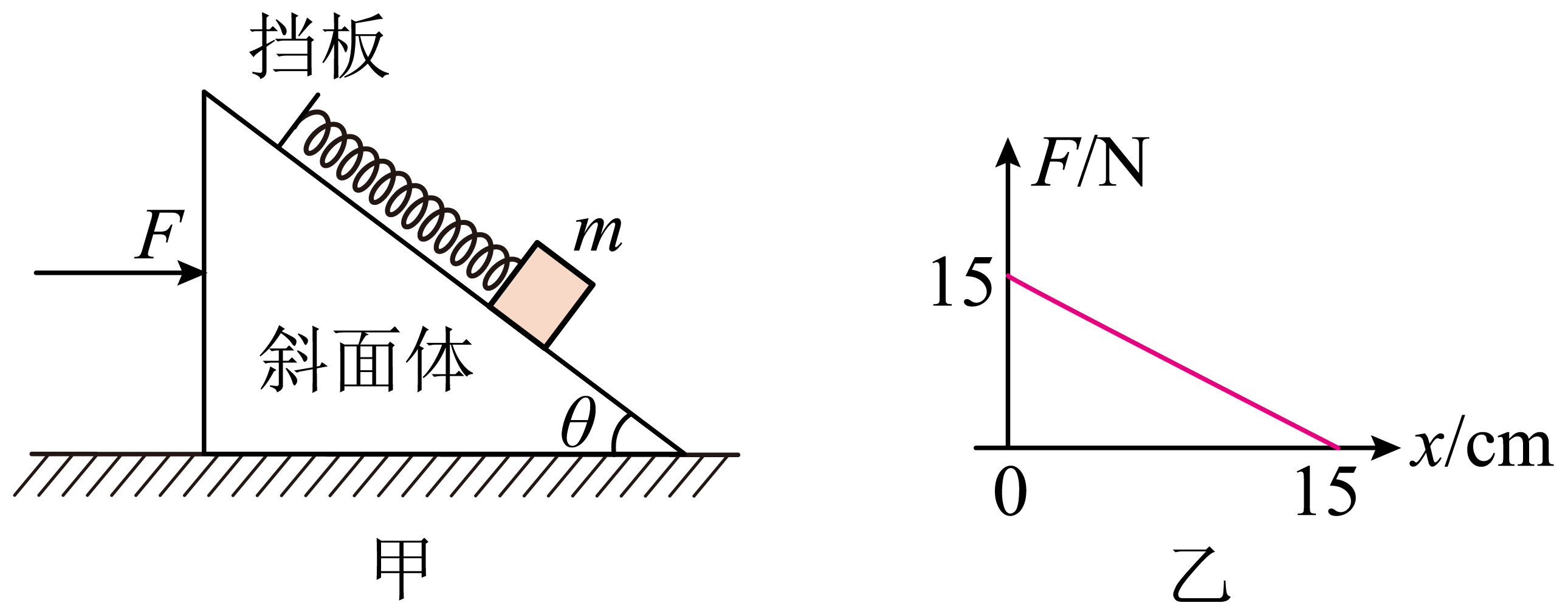
$1\\;\\rm kg$ $20\\;\\rm N/m$
","$1\\;\\rm kg$ $40\\;\\rm N/m$
","$2\\;\\rm kg$ $20\\;\\rm N/m$
","$2\\;\\rm kg$ $40\\;\\rm N/m$
"]当推力为$0$时,根据受力平衡结合胡克定律可知$mg\sin \theta=kx_{0}$
可得轻弹簧的劲度系数为$k=\dfrac{mg\sin\theta}{x_{0}}=\dfrac{1 \times 10 \times 0.6}{0.15}\;\text{N/m}=40\;\text{N/m}$
当弹簧处于原长时,对物块根据牛顿第二定律可得$F_{合}=mg\tan \theta=ma$
以物块和斜面为整体,根据牛顿第二定律可得$F=(M+m)a$
由图可知$F=15\;\rm N$,联立解得斜面体的质量为$M=1\;\rm kg$
故选:$\rm B$。
| 牛顿第二定律的两类基本问题题目答案及解析(完整版)
