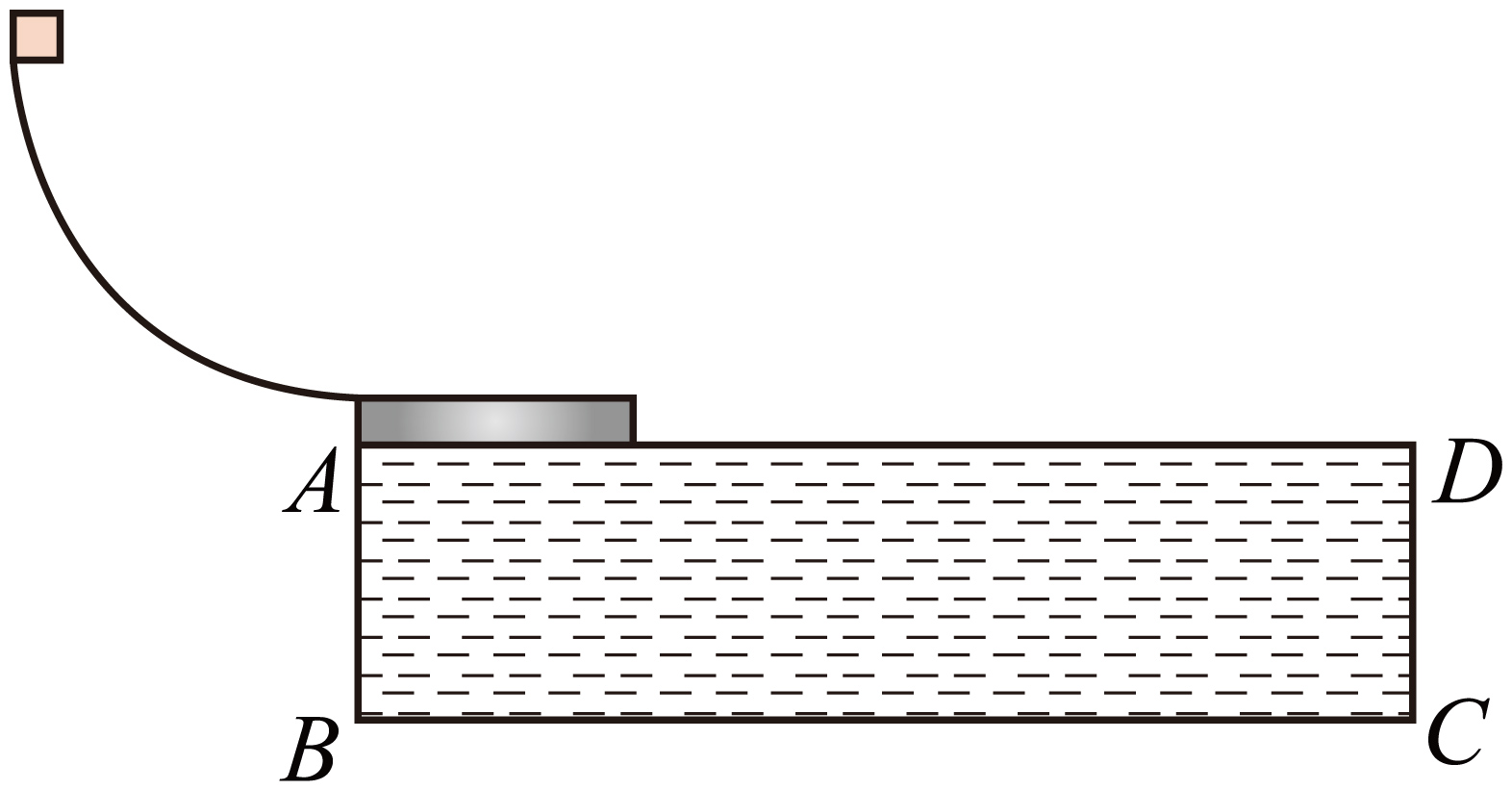
求小物块运动至轨道最底端时，轨道对其支持力的大小；

$3\\;\\rm N$；

由动能定理可得$mgR= \dfrac{1}{2}mv_{A}^{2}-0$，

小物块运动至轨道最底端时，由圆周运动公式可得$F_{{N}}-mg=m\dfrac{v_{A}^{2}}{R}$，

联立解得$F_{N}=3\;\rm N$；

若木板在水面上运动时水的阻力忽略不计，则小物块与木板达到共速时（木板尚未到达水池右端），求小物块与木板左端的距离；

$1.875\\;\\rm m$；

由动量守恒定律可得$mv_{A}=(M+m)v_{共}$，

由动能定理可得$- \mu mgx=\dfrac{1}{2}\text{(}M+m\text{)}v_{共}^{2}-\dfrac{1}{2}mv_{A}^{2}$，

小物块与木板左端的距离$x=1.875\;\rm m$；

若木板在水面上运动时，水对木板的阻力$f$与木板的速度$v$成正比，即$f=kv$，其中$k=0.25\;\rm kg/s$。最终木板恰好运动至水池右端速度减为零，且小物块也处在木板的右端，求水池的长度$L_{AD}$和整个过程中木板的最大速度$v_\rm{m}$。

$4\\;\\rm m$，$1\\;\\rm m/s$。

从开始到最终静止，对小物块和木板组成的整体，

由动量定理可得$−k\overline{v_{1}}\times t_{1}=0−mv_{A}$，

木板位移$x_{1}=\overline{v_{1}}t_{1}=2\ \rm m$，

水池的长度$L_{AD}=x_{1}+L=4\;\rm m$；

由分析可知当小物块与木板共速时，木板达到最大速度$v_{\rm m}$，之后小物块与木板相对静止一起减速到水池右端，则共速时小物块恰好运动到木板右端。

从开始到共速，对系统动量定理可得$-k\overline{v_{2}}t_{2}=\left( m+M\right)v_{\rm m}-mv_{A}$，

木板位移$x_{2}=\overline{v_{2}}t_{2}$，

对小物块由动能定理可得$-\mu mg\left( x_{2}+L\right)=\dfrac{1}{2}mv_{\rm m}^{2}-\dfrac{1}{2}mv_{A}^{2}$，

联立解得$v_{\rm m}=1\ \rm m/s$。