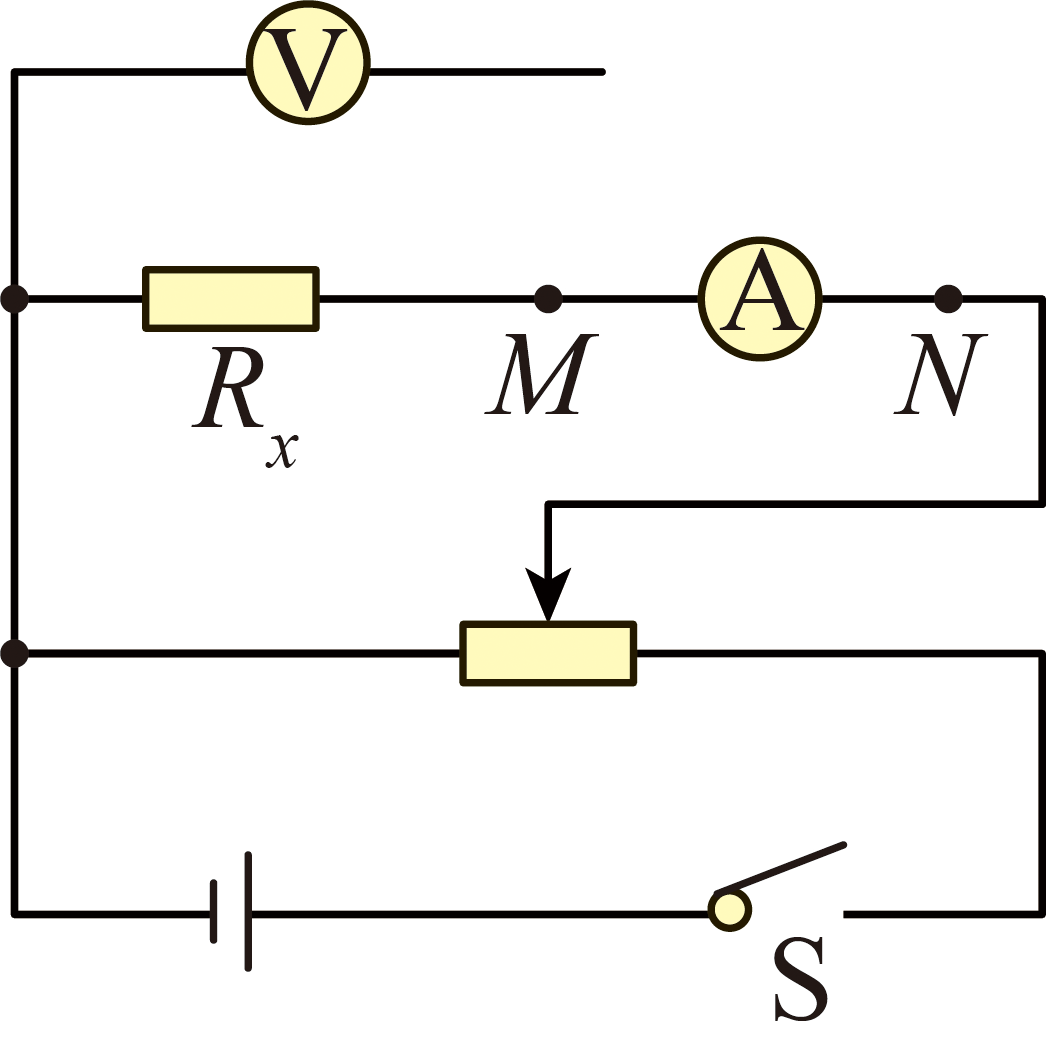
该同学采用如图所示的电路测量金属丝的电阻$R_{x}$。现有电源（电动势为3.0V，内阻不计），电压表（量程0~3V，内阻约3kΩ），开关和导线若干，以及下列器材。为了调节方便、测量准确，实验中电流表和滑动变阻器应选用$(\quad\ \ \ \ )$。（选填实验器材前的字母）

电流表（量程0~3A，内阻约0.025Ω）

电流表（量程0~0.6A，内阻约0.125Ω）

滑动变阻器（0~5Ω，3A）

滑动变阻器（0~1000Ω，0.5A）

根据题中信息可得流过电阻的最大电流约为$I_{\max}=\frac{U}{R}=\frac{3}{5}\text{A}= 0.6\text{A}$

为了减小误差，电流表选择B；

由题图可知滑动变阻器采用分压式连接，为了方便操作，选用最大阻值较小的C。

电压表应连接                 点（选填“M”或“N”）。闭合开关S前，滑动变阻器的滑片应处在                 （选填“左端”或“右端”）。

通过计算可得出$\frac{R_{\text{V}}}{R_{x}} \gt \frac{R_{x}}{R_{\text{A}}}$

为了减小误差，电压表应连接M点；

为了保护电路，闭合开关S前，滑动变阻器的滑片应处在使测量电路部分电压为零的左端。

测得金属丝的直径为d，长度为L，电阻为R，则该金属丝电阻率测量值的表达式$ρ=$                 。仅考虑电表内阻引起的误差，电阻率的测量值                 真实值（选填“大于”或“小于”）。

根据电阻定律$R= \rho\frac{L}{S}$

又$S=\pi{(\frac{d}{2})}^{2}$

联立可得$\rho=\frac{\pi d^{2}R}{4L}$

根据（2）中分析可知，电流表采用外接法，则电流的测量值大于流过电阻的真实值，根据欧姆定律$R= \frac{U}{I}$可知电阻的测量值小于真实值，则电阻率的测量值小于真实值。

材料的电阻率$ρ$随温度t变化的规律为$ρ=ρ_{0}(1+αt)$，其中$ρ_{0}$是材料在t=0℃时的电阻率，$α$为电阻温度系数，在一定的温度范围内$α$是与温度无关的常量。不同材料的$α$可能为正数也可能为负数。该同学设想利用两种材料制成阻值在一定温度范围内不随温度变化的电阻。若在0℃时，A材料的电阻率为$ρ_{01}$，电阻温度系数为$α_{1}$，B材料的电阻率为$ρ_{02}$，电阻温度系数为$α_{2}$。用A、B两种材料制成横截面积为S，长度分别为L₁和L₂的导线，将两段导线串联成一个导体，S、L₁、L₂均不随温度变化。当L₁、L₂满足                 关系时，导体的电阻在0℃附近不随温度变化，若使该导体的电阻等于R，则L₁、L₂与R的关系式为$R=$                 。

要使得两段导线串联成的个导体电阻不随温度发生变化，即两段导线电阻之和不变，即两段导线电阻随温度的变化率互为相反数，根据电阻定律得$R=\rho_{0}(1+\alpha t)\frac{L}{S}$

求导可得导线电阻随温度的变化率$\frac{\Delta R}{\Delta t}=\dfrac{\rho_{0}\alpha L}{S}$

即需要满足$ρ_{01}α_{1}L_{1}=−ρ_{02}α_{2}L_{2}$

整理可得$ρ_{01}α_{1}L_{1}+ρ_{02}α_{2}L_{2}=0$

根据电阻定律可得$R=\rho_{01}\left( 1+\alpha_{1}t \right)\frac{L_{1}}{S}+\rho_{02}\left( 1+\alpha_{2}t \right)\frac{L_{2}}{S}$

结合$ρ_{01}α_{1}L_{1}+ρ_{02}α_{2}L_{2}=0$

联立可得$R=\rho_{01}\frac{L_{1}}{S}+\rho_{02}\frac{L_{2}}{S}$