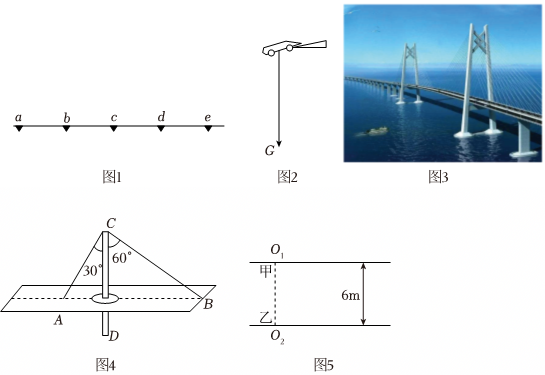
图$1$中$a$、$b$、$c$、$d$、$e$是五个连续等间距的桥墩，若一汽车从$a$点由静止开始做匀加速直线运动，通过$ab$段的时间为$t$，则通过$cd$段的时间为 _____ 。

$t$

$(\\sqrt{2}-1)t$

$(\\sqrt{3}-\\sqrt{2})t$

$(2-\\sqrt{3})t$

由题意可知$ab$、$ac$、$ad$的长度比为$1:2:3$，根据初速度为零的匀加速直线运动规律$x= \dfrac{1}{2}at^{2}$可知：$t= \sqrt{\dfrac{2x}{a}}$；所以汽车通过$ab$、$ac$、$ad$的所用的时间之比为$1:\sqrt{2}:\sqrt{3}$，通过$ab$段的时间为$t$，则通过$cd$段的时间为：$t_{cd}=t_{ad}-t_{ac}= \sqrt{3}t- \sqrt{2}t=(\sqrt{3}-\sqrt{2})t$，故$\rm C$正确，$\rm ABD$错误。

故选：$\rm C$。

大桥的引桥可视为斜面。某处引桥的角为$\theta$，引桥上行驶的汽车，所受重为$G$按效果可沿斜面和垂直斜面两方向分解，如图$2$所示，沿斜面方向的分力为 _____ 。

$G\\cos\\theta$

$G\\sin\\theta$

$\\dfrac{G}{\\cos\\theta}$

$\\dfrac{G}{\\sin\\theta}$

所受重为$G$按效果可沿斜面和垂直斜面两方向分解，如图所示，

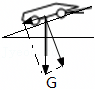
依据三角知识，则沿斜面方向的分力为$G_{1}=G\sin\theta$，故$\rm ACD$错误，$\rm B$正确；

故选：$\rm B$。

港珠澳大桥的所有钢索均处在同一竖直面内斜拉桥，其索塔与钢索如图$3$所示（不计钢索的质量）。下列说法正确的是：$(\quad\ \ \ \ )$。

增加钢索数量，可减小索塔受到总的拉力

适当降低索塔的高度，可以减小钢索承受的拉力

钢索对称，可以保证钢索对索塔拉力的合力为零

钢索对称，可以保证钢索对索塔拉力的合力偏离竖直方向不至于过大

$\rm A$．对桥身进行受力分析可知，钢索对桥身的拉力的合力与桥身的重力大小相等、方向相反，则钢索对索塔向下的压力数值上等于桥身的重力，与钢索数量无关，故$\rm A$错误；

$\rm B$．对桥身进行受力分析可知，钢索对桥身的拉力的合力与桥身的重力大小相等、方向相反，则钢索对索塔向下的压力数值上等于桥身的重力，合力一定，分力间的夹角越小，则分力越小，为了减小钢索承受的拉力，应该增大索塔的高度，达到减小钢索间夹角的目的，故$\rm B$错误；

$\rm CD$．根据对称性可知，索塔两侧钢索对称分布，拉力大小相等时，水平分力基本抵消，可以保证钢索对索塔拉力的合力偏离竖直方向不至于过大，使得钢索对索塔的合力基本上是竖直向下，故$\rm C$错误、$\rm D$正确。

故选：$\rm D$。

港珠澳大桥可用如图$4$模型研究：细杆$CD$固定在地面，从质量为$m$的均匀平板正中央空洞内穿过。通过两根轻质细线$CA$、$CB$将平板水平悬挂，与竖直方向夹角分别为$30^\circ$、$60^\circ$。则$CB$绳对平板的拉力大小为                  ；保持平板水平不动，逐渐缩短$CB$线，使悬挂点$B$左移，$CB$绳对平板的拉力将                  （选填“$\rm A$：变大”“$\rm B$：变小”“$\rm C$：先变大后变小”或“$\rm D$：先变小后变大”）。

对$C$点进行受力分析，如图所示：

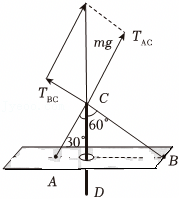
根据几何关系可得：$T_{BC}= \dfrac{1}{2}mg$

根据几何关系可知，当悬挂点$B$左移，则$BC$边会逐渐边长，因此$CB$绳对平板的拉力将变大，故$\rm A$正确、$\rm BCD$错误。

港珠澳大桥上甲，乙两辆汽车在各自车道上做直线运动，（如图$5$）$t=0$时，甲车以$10\;\rm m/s$的速度经过$O_{1}$点，乙车以$1\;\rm m/s$的速度经过$O_{2}$点。此时关闭甲车动力，甲车以$2\;\rm m/s^{2}$的加速度向右做匀减速直线运动，乙车继续向右做匀速直线运动。已知$O_{1}O_{2}$与轨道垂直，两车间的距离超过$10\;\rm m$时他们将无法通过蓝牙实现通信，忽略信号传递的时间，则当两车之间的距离为$10\;\rm m$时，它们沿平行轨道方向的相对距离为                  $\rm m$，从$t=0$起两车间能通信的时间共为                  $\rm s$。

当两车之间的距离为$10\;\rm m$时，它们沿平行轨道方向的相对距离为：$\Delta x= \sqrt{L_{m}^{2}-d^{2}}=\sqrt{10^{2}-6^{2}}\;\rm m=8\;\rm m$

当二者之间沿导轨方向的距离大于$8\;\rm m$时，不能实现通信。

开始时$A$的速度$v_{1}=10\;\rm m/s$，$B$的速度$v_{2}=1\;\rm m/s$；

设经过时间$t$，两车沿导轨相距$\Delta x.$由运动学规律 $A$车的位移$s_{A}= v_{1}t-\dfrac{1}{2}at^{2}$

$B$车的位移：$s_{B}=v_{2}t$

由空间几何关系：$s_{A}-s_{B}=\Delta x$；

联立，有$t^{2}-9t+8=0$

解得：$t_{1}=1\;\rm s$，$t_{2}=8\;\rm s$

但$A$车的速度减为零的时间：$t_{0}$$= \dfrac{v_{1}}{a}=\dfrac{10}{2}\;\rm s=5\;\rm s$

可知在$5\;\rm s$末$A$车已停止运动，$t_{2}=8\;\rm s$舍去；可知在$5\;\rm s$前$A$与$B$能通讯的时间为$1\;\rm s$；

当$t_{2}=5\;\rm s$时，$A$的位移：$x_{0}= \dfrac{v_{1}}{2}t_{0}=\dfrac{10}{2} \times 5\;\rm m=25\;\rm m$

根据空间关系，$A$的位移是$25\;\rm m$，当$B$与$A$之间的沿导轨之间的距离为$8\;\rm m$时，即$B$的位移为$x_{1}=x_{0}-\Delta x=25\;\rm m-8\;\rm m=17\;\rm m$或$x_{2}=x_{0}+\Delta x=25\;\rm m+8\;\rm m=33\;\rm m$

对应两个位移$B$运动的时间：$t_3= \dfrac{x_{1}}{v_{2}}=\dfrac{17}{1}\;\rm s=17\;\rm s$；$t_4= \dfrac{x_{2}}{v_{2}}=\dfrac{33}{1}\;\rm s=33\;\rm s$

显然，两车通信的第二个时间段为$\Delta t=t_{4}-t_{3}=33\;\rm s-17\;\rm s=16\;\rm s$，故两车能通信的时间为：$t_{总}=t_{1}+\Delta t=1\;\rm s+16\;\rm s=17\;\rm s$。