高中 | 闭合电路的欧姆定律基本问题 题目答案及解析
稿件来源:高途
高中 | 闭合电路的欧姆定律基本问题题目答案及解析如下,仅供参考!
选修3-1
第二章 恒定电流
2.7 闭合电路的欧姆定律
闭合电路的欧姆定律基本问题
传感器在现代生活中有着广泛的应用。某同学利用压力传感器设计了一个台秤,其电路图如图$1$所示。$R$为压敏电阻,其阻值与所受压力大小$F$的关系如图$2$所示。
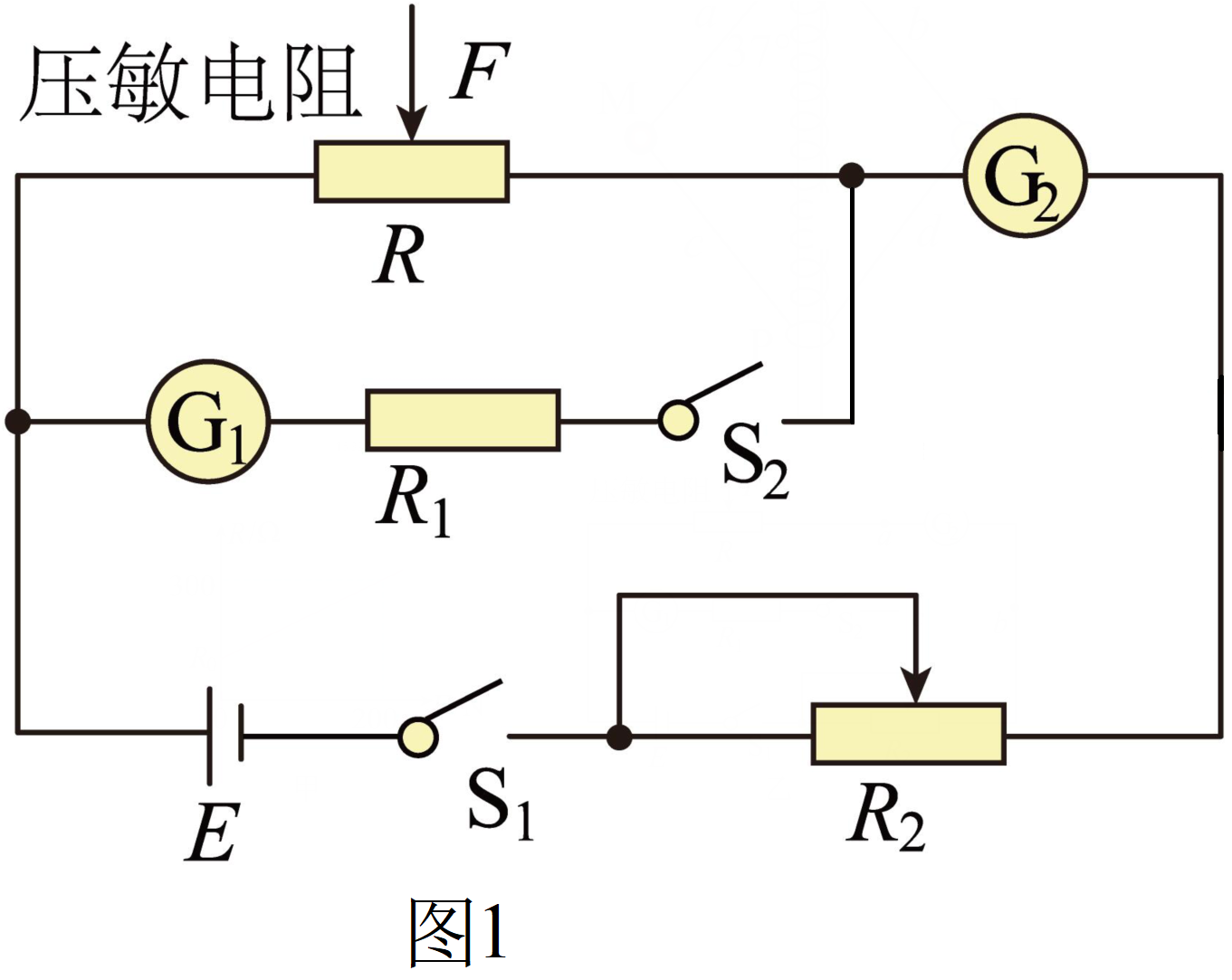

实验主要器材如下:
压敏电阻$R$($F=0$时的阻值$R_{0}$在$50\;\rm \Omega ∼ 90\;\rm \Omega$之间);
电源(电动势$E=6\;\rm V$,内阻约几欧);
电流表$\rm G_{1}$(量程$10\;\rm mA$,内阻$R_{g1}=100\;\rm \Omega$);
电流表$\rm G_{2}$(量程$30\;\rm mA$,内阻$R_{g2}$约$100\;\rm \Omega$);
定值电阻$R_{1}$,阻值为$100\;\rm \Omega$;
滑动变阻器$R_{2}$,最大电阻值为$100\;\rm \Omega$;
开关$\rm S_{1}$,$\rm S_{2}$及导线若干。
实验操作如下:
①按图示方法连接电路;
②闭合开关$\rm S_{1}$,$\rm S_{2}$,对压敏电阻$R$不施加压力,调节滑动变阻器接入电路的阻值,当电流表$\rm G_{2}$读数为$26\;\rm mA$时,电流表$\rm G_{1}$读数为$6.0\;\rm mA$,测出压敏电阻在没有压力时的阻值为$R_{0}$;
③断开开关$\rm S_{2}$,调节滑动变阻器$R_{2}$,使电流表$\rm G_{2}$达到满偏,满偏电流刻度处标记$F=0$;
④保持滑动变阻器阻值不变,在压敏电阻上施加力$F$,在$\rm G_{2}$对应的电流处标出压力$F$的值。
根据实验操作,回答下列问题:
闭合开关$\rm S_{1}$,$\rm S_{2}$进行实验前,滑动变阻器的滑动触头应处在 (填“最左端”或“最右端”);
闭合开关$\rm S_{1}$,$\rm S_{2}$进行实验前,滑动变阻器的滑动触头应处在最左端,接入的电阻最大,起到保护电路的作用;
由实验可知压敏电阻在无压力时的阻值$R_{0}=$ $\;\rm \Omega$;
由并联电路的特点可知$I_{1}(R_{1}+R_{g1})=(I − I_{1})R_{0}$
可得$R_{0}=\dfrac{I_{1}(R_{1}+R_{g1})}{I-I_{1}}=\dfrac{6 \times (100+100)}{26-6}\Omega=60\;\rm \Omega$;
在步骤④中,当电流表$\rm G_{2}$示数为$25\;\rm mA$时压敏电阻受到的压力$F=$ $\;\rm N$;
由闭合电路欧姆定律$E=I_{2m}(R_{0}+R_{2}+R_{g2}+r)$
可得$R_{2}+R_{g2}+r=\dfrac{E}{I_{2{m}}}-R_{0}=\dfrac{6}{30 \times 10^{- 3}}\;\rm \Omega-60\;\rm \Omega=140\;\rm \Omega$
则电流为$25\;\rm mA$时,压敏电阻为
$R=\dfrac{E}{I_{2}}-(r++ R_{2}+R_{{g}2})=\dfrac{6}{25 \times 10^{- 3}}\;\rm \Omega-140\;\rm \Omega=100\;\rm \Omega$
$R-F$图像的斜率为$k=\dfrac{300-60}{200}\;\rm \Omega/N=\dfrac{6}{5}\;\rm \Omega/N$
根据图甲,压敏电阻$R$与压力$F$的关系式$R=60+\dfrac{6}{5}F$
可得$F=\dfrac{100}{3}\;\rm {N}$;
若电池使用一段时间后电动势减小,在没有压力时调整滑动变阻器的滑动触头使电流表$\rm G_{2}$满偏,则再次使用时测得的压力值 (填“偏大”“偏小”或“与真实值相等”)。
由以上分析可知若电池使用一段时间后电动势减小,在没有压力时调整滑动变阻器的滑动触头使电流表$\rm G_{2}$满偏,滑动变阻器接入的阻值变小,所用计算出的压敏电阻偏大,则导致计算出的压力偏大。
高中 | 闭合电路的欧姆定律基本问题题目答案及解析(完整版)
