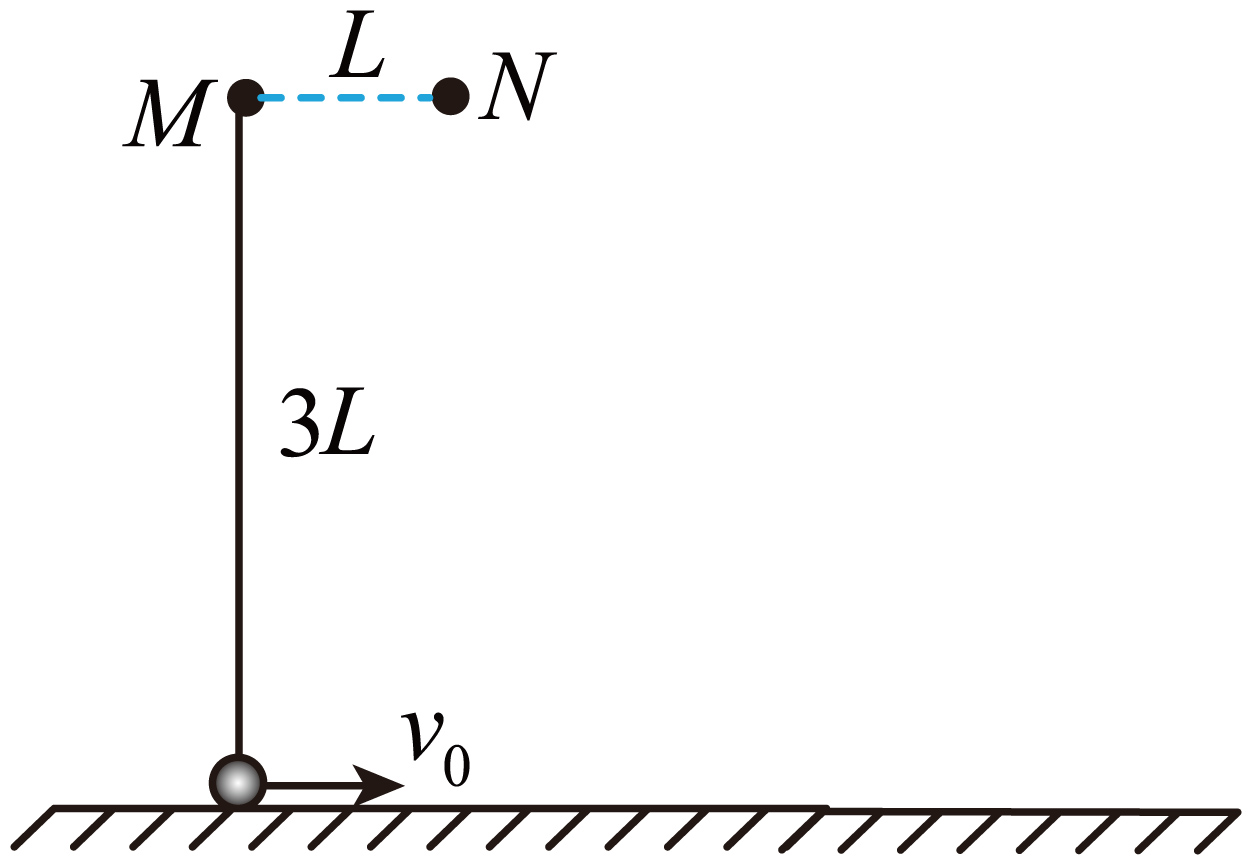
求绳子被拉断时小球的速度大小，及绳子所受的最大拉力大小；

$v= 4\\sqrt{5}\\;\\rm{m/s}$，$T=17\\;\\rm N$；

小球从最下端以速度$v_{0}$抛出到运动到$M$正下方距离为$L$的位置时，根据机械能守恒定律$\dfrac{1}{2}mv_{0}^{2}=mg \cdot 2L+ \dfrac{1}{2}mv^{2}$

在该位置时根据牛顿第二定律$T-mg=m\dfrac{v^{2}}{L}$

解得$v=4\sqrt{5}\;\rm{m/s}$，$T=17\;\rm N$；

求小球做平抛运动时抛出点到落地点的水平距离；

$4\\;\\rm m$；

小球做平抛运动时$x=vt$，$2L=\dfrac{1}{2}gt^{2}$

解得$x=4\;\rm m$；

若在$t=0$时，只改变小球的初速度大小，使小球能通过$N$的正上方且绳子不松弛，求初速度的最小值。

$2\\sqrt{15}\\;\\rm{m/s}$。

若小球经过$N$点正上方绳子恰不松弛，则满足$mg=m\dfrac{v^{'2}}{2L}$

从最低点到该位置由动能定理$\dfrac{1}{2}mv_{0}^{'2}=mg \cdot 5L+\dfrac{1}{2}mv^{'2}$

解得$v_{0}'=2\sqrt{15}\;\rm{m/s}$。