若物块从$a$点运动到$c$点所用时间为$t_{0}$，则在$0.5t_{0}$时，物块在$(\quad\ \ \ \ )$

$A$段

$B$点

$C$段

$D$点

$E$段

物块从$a$点运动到$c$点过程中一直做减速运动，可知沿圆弧物块$a$点运动到$b$点的平均速率大于$b$点运动到$c$点的平均速率。若物块从$a$点运动到$c$点所用时间为$t_{0}$，则在$0.5t_{0}$时，物块在$E$段。故$\rm ABCD$错误，$\rm E$正确；

故选：$\rm E$；

若物块在$a$点的速度为$v_{0}$，经过时间$t$刚好到达$b$点，则在该过程中轨道对物块的支持力的冲量为$(\quad\ \ \ \ )$

$mv_{0}$

$mgt$

$mv_{0}+mgt$

$m\\sqrt{v_{0}^{2}+g^{2}t^{2}}$

以初速度方向为正方向，根据动量定理，支持力在水平方向的冲量为$I_{x}=0-mv_{0}$

竖直方向上根据动量定理有$I_{y}-mgt=0$

故该过程中轨道对物块的支持力的冲量为：$I=\sqrt{I_{x}^{2}+I_{x}^{2}}=m\sqrt{v_{0}^{2}+g^{2}t^{2}}$

故$\rm ABC$错误，$\rm D$正确；

故选：$\rm D$；

若物块质量为$0.5\;\rm kg$，下图是物块的速度$v$与物块和圆心连线转过的夹角$\theta$的关系图像。

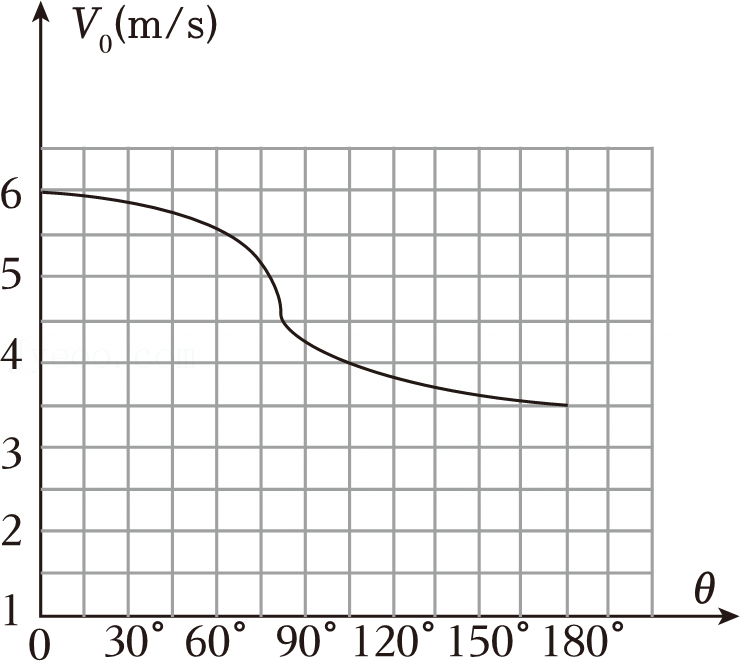
①求轨道半径$R$；

②求$\theta=60^\circ$时，物块克服重力做功的瞬时功率$P$。

①轨道半径$R$为$0.59\\;\\rm m$；②物块克服重力做功的瞬时功率$P$为$23.8\\;\\rm W$

①由图像可知，物块的初速度为$6\;\rm m/s$，最高点位置的速度为$3.5\;\rm m/s$。由动能定理得$- mg2R=\dfrac{1}{2}mv^{2}- \dfrac{1}{2}mv_{0}^{2}$

解得$R=0.59\;\rm m$

②由图像可知$\theta=60^\circ$时，物块的速度为$5.5\;\rm m/s$，则物块克服重力做功的瞬时功率$P=mgv\sin60^\circ$

解得$P≈23.8\;\rm W$。