如图所示，空间有垂直于坐标系$xOy$平面向外的匀强磁场。$t=0$时，带电粒子$a$从$O$点沿$x$轴负方向射出；$t_{1}$时刻，$a$与静置于$y$轴上$P$点的靶粒子$b$发生正碰，碰后$a$、$b$结合成粒子$c$，$t_{2}$时刻，$c$第一次沿$y$轴负方向通过$x$轴上的$Q$点。已知$t_{1}:t_{2}=1:6$，不考虑粒子间静电力的作用，忽略碰撞时间，则$(\qquad)$

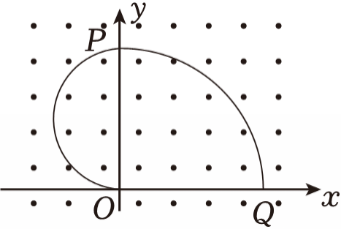
$b$粒子带负电

$a$和$c$的电荷量之比为$1:2$

$a$和$c$的速率之比为$5:2$

$a$和$b$的质量之比为$1:4$

$\rm C$、设$OP=2r$，$a$、$b$碰撞前后做匀速圆周运动的时间分别为$t_{1}=\dfrac{1}{2}T_{1}=\dfrac{2\pi r}{2v_{1}}$

$t_{2}-t_{1}=\dfrac{1}{4}T_{2}=\dfrac{2\pi \cdot 2r}{4v_{2}}$

联立解得$a$和$c$的速率之比为$\dfrac{v_{1}}{v_{2}}=\dfrac{5}{1}$，故$\rm C$错误；

$\rm D$、$a$、$b$发生碰撞，取向右为正方向，根据动量守恒定律得

$m_{a}v_{1}=(m_{a}+m_{b})v_{2}$

解得$\dfrac{m_{a}}{m_{b}}=\dfrac{1}{4}$，故$\rm D$正确；

$\rm AB$、设$a$粒子电荷量为$q_{1}$，$b$粒子电荷量为$q_{2}$。$a$粒子做匀速圆周运动，根据洛伦兹力提供向心力有$q_{1}v_{1}B=m_{a}\dfrac{v_{1}^{2}}{r}$

$c$粒子做匀速圆周运动，根据洛伦兹力提供向心力有$(q_{1}+q_{2})v_{2}B=(m_{a}+m_{b})\dfrac{v_{2}^{2}}{2r}$

解得$q_{2}=- \dfrac{1}{2}q_{1}$

根据左手定则，可知粒子$a$带正电，则粒子$b$带负电，粒子$c$带正电，$a$和$c$的电荷量之比为$q_{1}:(q_{1}+q_{2})=2:1$，故$\rm A$正确，$\rm B$错误。

故选：$\rm AD$。