高中 | 动量守恒定律的理解与一般应用 题目答案及解析
稿件来源:高途
高中 | 动量守恒定律的理解与一般应用题目答案及解析如下,仅供参考!
选修3-5
第十六章 动量守恒定律
16.3 动量守恒定律
动量守恒定律的理解与一般应用
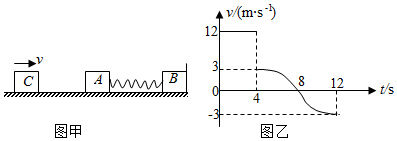
如图甲所示,物块$B$和质量为$m_{A}=6.0\;\rm kg$的物块$A$用轻弹簧拴接,放在光滑的水平地面上,物块$B$右侧与竖直墙相接触。另有一物块$C$在$t=0$时刻以一定速度向右运动,在$t=4\;\rm s$时与物块$A$相碰,并立即与$A$粘在一起不再分开,物块$C$的$v-t$图像如图乙所示。求:
物块$C$的质量$m_{C}$;
$2\\;\\rm kg$
"]]由图乙可知,$C$与$A$碰前速度为 $v_{1}=12\;\rm m/s$,碰后速度为:$v_{2}=3\;\rm m/s$,$C$与$A$碰撞过程动量守恒,以碰撞前$C$的速度$v_{1}$的方向为正方向,由动量守恒定律可得:$m_{C}v_{1}=(m_{A}+m_{C})v_{2}$,解得:$m_{C}=\dfrac{m_{A}v_{2}}{v_{1}-v_{2}}= \dfrac{6.0 \times 3}{12-3}\;\rm kg=2\;\rm kg$;
物块$C$与物块$A$相碰过程中系统损失的机械能$E_{1}$;
$108\\;\\rm J$
"]]由能量守恒定律可得物块$C$与物块$A$相碰过程中系统损失的机械能为:
$E_{1}=\dfrac{1}{2}m_{C}v_{1}^{2}-\dfrac{1}{2}(m_{A}+m_{C})v_{2}^{2}=\dfrac{1}{2} \times 2 \times 12^{2}\;\rm J-\dfrac{1}{2} \times (2+6) \times 3^{2}\;\rm J=108\;\rm J$;
从$t=4\;\rm s$到$t=12\;\rm s$,弹簧对物块$A$的冲量$I$的大小。
$48\\;\\rm N\\cdot s$
"]]从$t=4\;\rm s$到$t=12\;\rm s$的过程中,对$A$、$C$组成的整体,以$v_{2}$的方向为正方向,则$t=12\;\rm s$时速度为,$v_{3}=-3\;\rm m/s$,
由动量定理可得:$I=(m_{A}+m_{C})v_{3}-(m_{A}+m_{C})v_{2}$,代入数据解得:$I=-48\;\rm N\cdot s$,可知弹簧对物块$A$的冲量$I$的大小为$48\;\rm N\cdot s$。
高中 | 动量守恒定律的理解与一般应用题目答案及解析(完整版)
