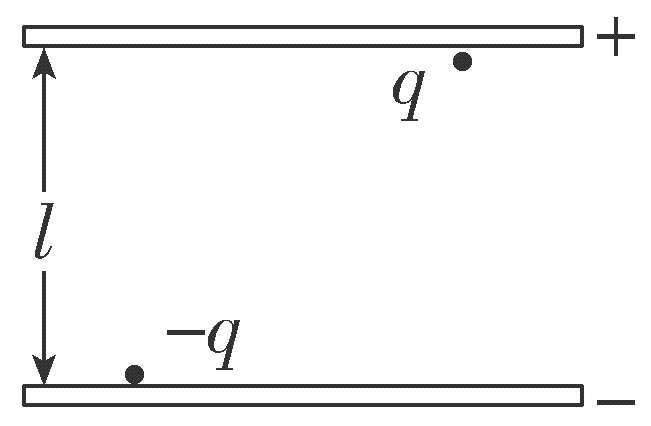
如图所示，一充电后的平行板电容器的两极板相距$l$。在正极板附近有一质量为$M$、电荷量为$q(q\gt 0)$的粒子；在负极板有另一质量为$m$、电荷量为$-q$的粒子。在静电力的作用下，两粒子同时从静止开始运动。已知两粒子同时经过平行于正极板且与其相距$\dfrac{2}{5}$$l$的平面。若两粒子间的相互作用可忽略，不计重力，则$M$∶$m$为$(\qquad)$

$3:2$

$2:1$

$5:2$

$3:1$

设平行板电容器内部电场强度为$E$，质量为$M$、电荷量为$q(q\gt 0)$的粒子运动的加速度为$a_{1}$，位移为$x_{1}$， 质量为$m$、电荷量为$-q$的粒子运动的加速度为$a_{2}$，位移为$x_{2}$，根据题意可知两粒子运动的位移之比为$\dfrac{x_{1}}{x_{2}}=\dfrac{\dfrac{2}{5}l}{\dfrac{3}{5}l}=\dfrac{2}{3}$，两粒子都从静止开始在电场力的作用下做匀加速直线运动，且运动时间相同，根据位移公式$x=\dfrac{1}{2}at^{2}$，可得两粒子运动的加速度之比为$\dfrac{a_{1}}{a_{2}}=\dfrac{x_{1}}{x_{2}}=\dfrac{2}{3}$；根据牛顿第二定律方程$Eq=ma$，可得两粒子的质量之比为$\dfrac{M}{m}=\dfrac{a_{2}}{a_{1}}=\dfrac{3}{2}$，故$\rm A$正确，$\rm BCD$错误。

故选：$\rm A$。