| 匀变速直线运动的速度位移公式 题目答案及解析
稿件来源:高途
| 匀变速直线运动的速度位移公式题目答案及解析如下,仅供参考!
必修1
第二章 匀变速直线运动的研究
2.4 匀变速直线运动的速度与位移的关系
匀变速直线运动的速度位移公式
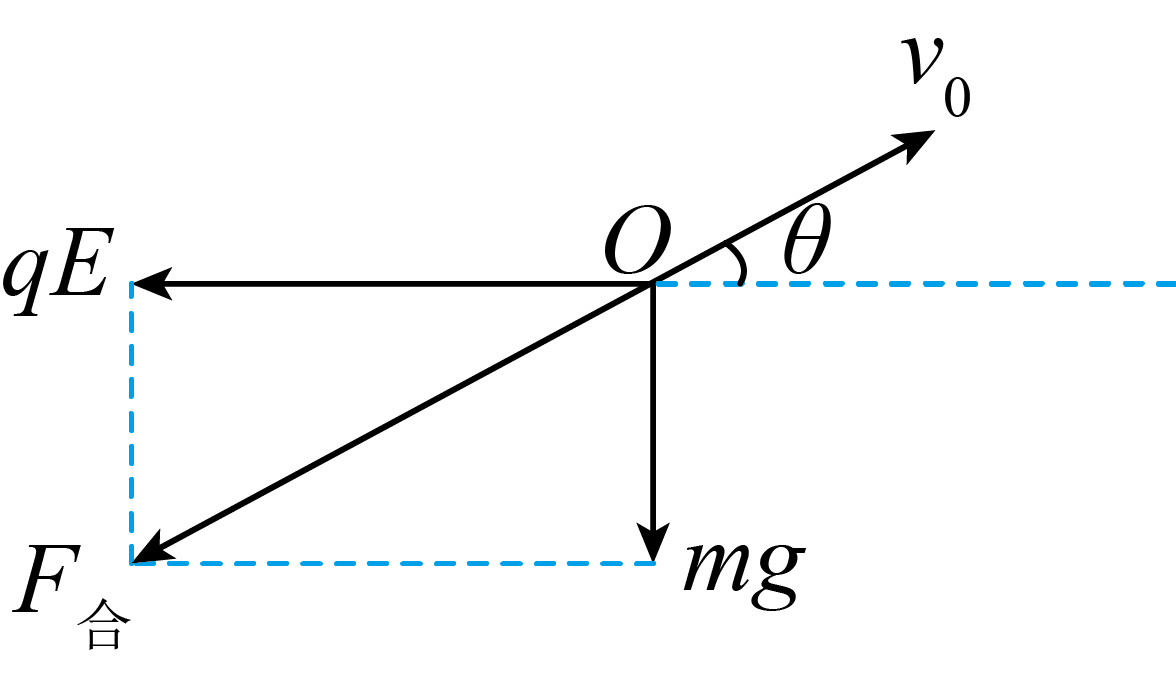
在学校物理创新实验课堂上,老师为引导学生探究带电物体在复合场中的运动规律,布置了一个如图所示的实验环境:空间中有一水平向左的匀强电场(电场空间足够大),将一个质量$m=0.3\;\rm kg$,电荷量$q=0.8\;\rm C$的带正电小球,放在区域内的$O$点,然后用弹射器使小球以$v_{0}=10\;\rm m/s$的初速度,方向与水平方向成$\theta=37^\circ$角斜向右射出,带电小球在电场力与重力作用下做直线运动($\sin37^\circ=0.6$,$\cos37^\circ=0.8$,$g$取$10\;\rm m/s^{2}$)。求:

电场强度$E$的大小;
$E=5\\;\\rm N/C$
"]]因小球做直线运动,受到竖直向下的重力$mg$和水平向左的电场力$qE$的合力必沿此直线,如图,由图可得$mg=qE\tan \theta$,所以$E=5\;\rm N/C$
小球从开始运动到最高点时,电势能的变化量$\Delta E_{P}$;
$\\Delta E_{p}=9.6\\;\\rm J$
"]]设从$O$点到最高点的位移为$x$,由运动学公式$0-v_{0}^{2}=2(-a)x$,根据牛顿第二定律可得$\dfrac{mg}{\sin\theta}=ma$
所以$x=\dfrac{v_{0}^{2}\sin\theta}{2g}$,小球运动到最高点时其电势能与在$O$点时的电势能之差为$W_{电}=- Eqx\cos\theta=- \dfrac{mv_{0}^{2}\cos^{2}\theta}{2}$
解得$\Delta E_{p}=-W_{电}=9.6\;\rm J$
若电场方向变成水平向右,小球仍以原来初速度从$O$点出发,当小球再次回到与$O$点同一水平面上的$A$点(未画出)时,求$OA$两点间电势差$U$的大小。
$U=96\\;\\rm V$
"]]若电场方向水平向右,则在竖直方向有$v_{0}\sin \theta=gt$,小球再次回到与$O$点同一水平面所用的时间为$t'=2t$,由牛顿第二定律可得$qE=ma$,根据运动的分解可得$v_{x}=v_{0}\cos 37^\circ =8\;\rm m/s$,由运动学规律可得$x=v_{x}t'+ \dfrac{1}{2}at'^{2}$,联立解得电势差$U=E\cdot x=96\;\rm V$
| 匀变速直线运动的速度位移公式题目答案及解析(完整版)
