| 示波管 题目答案及解析
稿件来源:高途
| 示波管题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
示波管
示波器中的示波管是利用电场来控制带电粒子的运动。如图甲所示,电子枪释放的无初速度电子被$U_{0}$的电场加速后进入偏转系统,若只考虑电子沿$Y$(竖直)方向的偏转情况,偏转系统可以简化为如图乙所示的偏转电场,偏转电极的极板长为$L_{1}$,两板间距离为$d$,极板右端与荧光屏的距离为$L_{2}$,当在偏转电极上加如图丙所示的电压时,电子在荧光屏产生亮线的最大长度为$L_{m}$。所有电子均能从极板射出打中荧光屏,且电子穿过极板的时间极短,可认为穿越过程中极板电压不变。已知电子的质量为$m$,电荷量为$e$,重力不计。求:
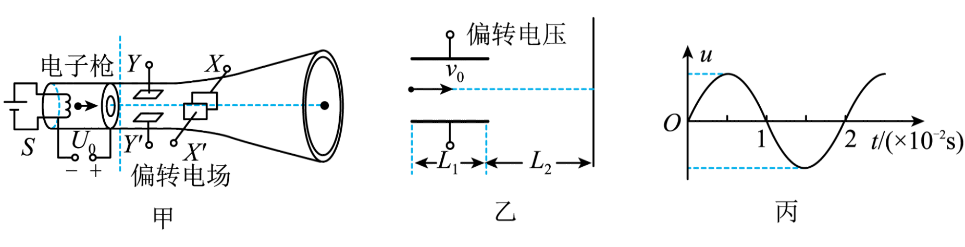
电子进入偏转电场速度$v_{0}$的大小;
$v_{0}= \\sqrt{\\dfrac{2\\text{eU}_{0}}{m}}$
"]]电子在加速电场中,由动能定理得$\dfrac{1}{2}mv_{0}^{2}=eU_{0}$,解得$v_{0}=\sqrt{\dfrac{2eU_{0}}{m}}$
电子最大偏转角的正切值;
$\\tan\\theta=\\dfrac{L_{\\text{m}}}{2L_{2}+ L_{1}}$
"]]电子在偏转场中做类平抛运动,出偏转场后做匀速直线运动,当打到荧光屏产生亮线的最下端或最上端时,偏转角最大,当打到最下端时,根据平抛运动末速度反向延长线过水平位移的中点可知,轨迹如图所示
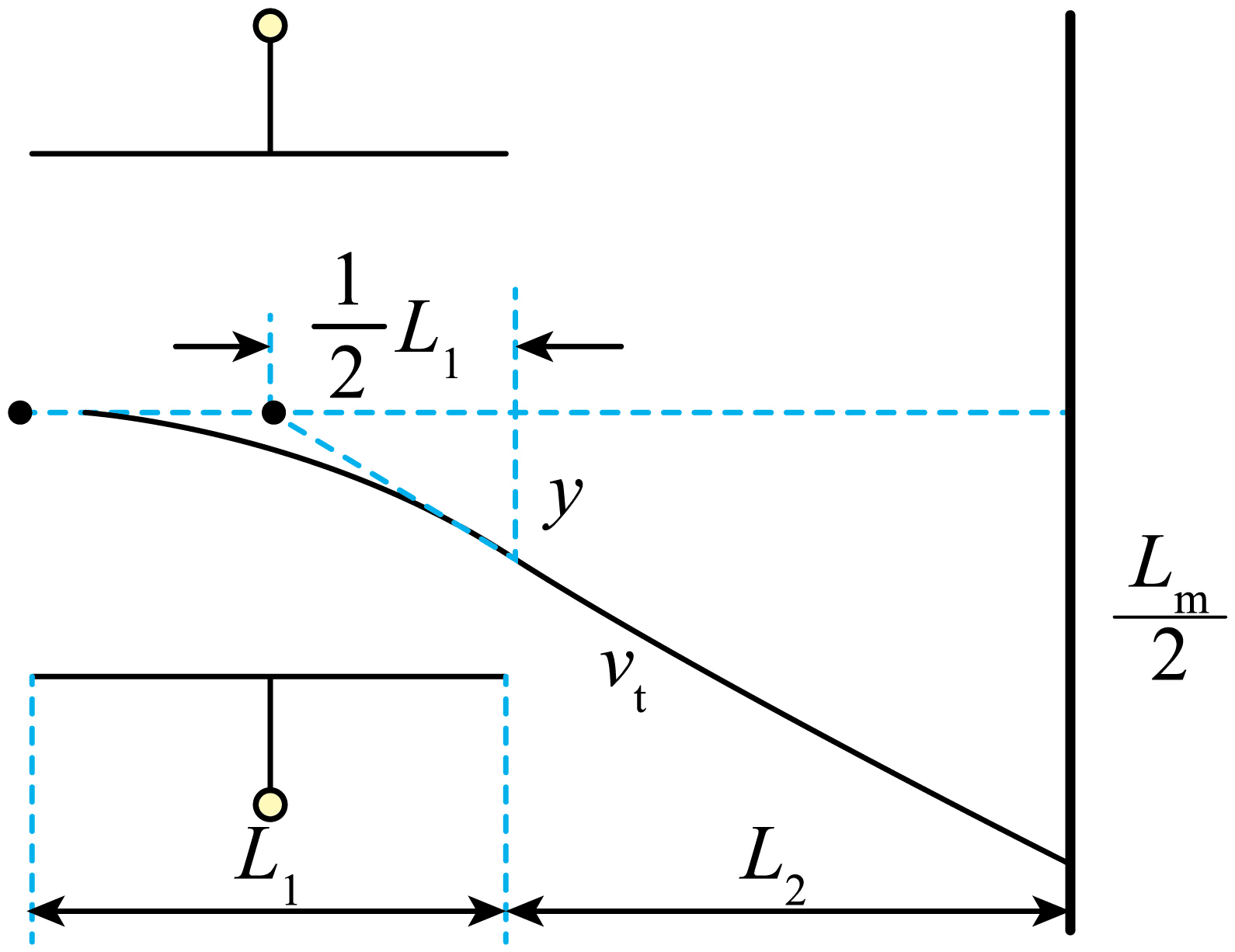
由几何关系可知$\tan\theta=\dfrac{\dfrac{L_{\text{m}}}{2}}{L_{2}+\dfrac{L_{1}}{2}}=\dfrac{L_{\text{m}}}{2L_{2}+L_{1}}$
丙图中的最大电压$U_{m}$。
$U_{\\text{m}}= \\dfrac{2L_{\\text{m}}dU_{0}}{\\left( L_{1}+2L_{2} \\right)L_{1}}$
"]]当偏转电压最大时,偏转角最大,此时水平方向$L_{1}=v_{0}t$,竖直方向的加速度为$a= \dfrac{eU_{\text{m}}}{dm}$,偏转的位移为$y= \dfrac{1}{2}at^{2}$,由($2$)中轨迹图,由几何关系$\tan\theta= \dfrac{y}{\dfrac{L_{1}}{2}}$,解得$U_{\text{m}}=\dfrac{2L_{\text{m}}dU_{0}}{\left( L_{1}+2L_{2} \right)L_{1}}$
| 示波管题目答案及解析(完整版)
