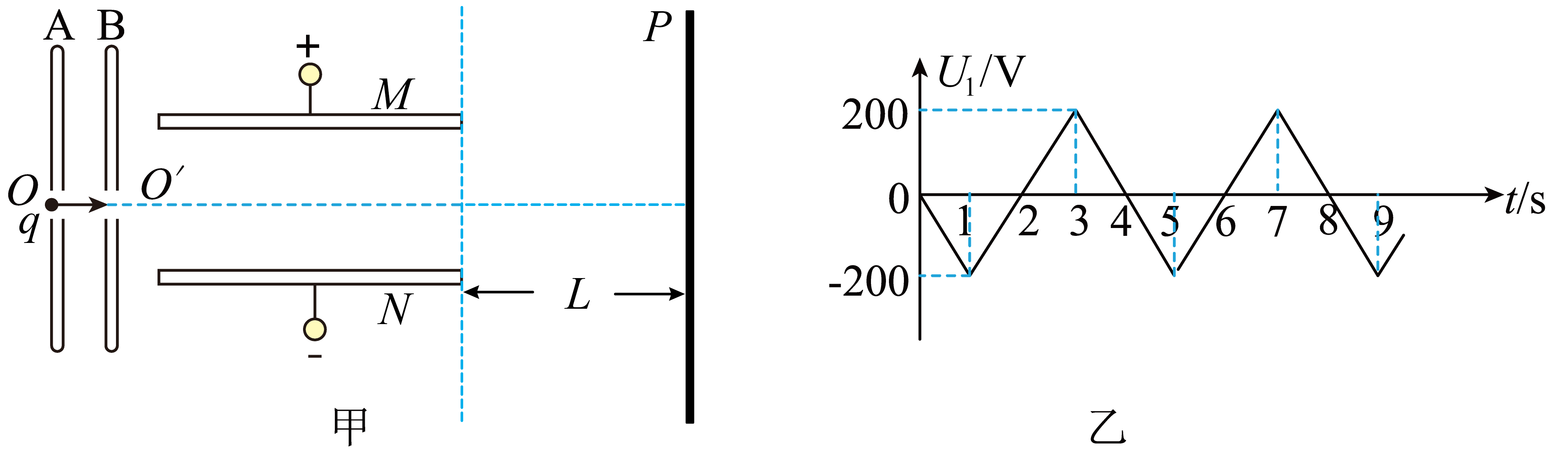
$0-4\;\rm s$内，哪些时间段有粒子从$B$板小孔$O'$射出？

$0\\lt t\\lt 0.5\\;\\rm s$和$1.5\\;{\\rm s}\\lt t\\lt 4\\;\\rm s$，粒子可以穿出

粒子带正电，在电场作用下减速至$0$，$E_{0}=Uq$，解得$U=100\;\rm V$，则$0\lt t\lt 0.5\;\rm s$和$1.5\;{\rm s}\lt t\lt 4\;\rm s$，粒子可以穿出。

$t=0$时刻从小孔$O$射入的粒子，

①在偏转电场中的偏转量$y$；

②穿出偏转电场时的动能$E_{k}$；

①$y=0.01\\;\\rm m$；②$E_{k}=0.0104\\;\\rm J$

①$t=0$时刻从小孔$O$进入的粒子，初动能为$E_{0}=1 \times 10^{-2}\;\rm J$，在偏转电场，竖直方向有$y=\dfrac{1}{2}at^{2}=\dfrac{1}{2} \cdot \dfrac{U_{2}qL^{2}}{mdv_{0}^{2}}$，其中$E_{\text{0}}= \dfrac{1}{2}mv_{0}^{2}$，解得$y=0.01\;\rm m$

②由动能定理可知$E_{\text{k}}=E_{0}+\dfrac{U_{2}qx}{d}$，则$E_{k}=0.0104\;\rm J$

接收屏$P$被粒子打中区域的长度$l$。

$5\\;\\rm cm$

粒子在$t=3\;\rm s$射入偏转电场时动能最大，在电场中的偏转量最小，则$E_{k}=E_{0}+qU_{1}=3 \times 10^{-2}\;\rm J$

竖直方向有$y_{\min}=\dfrac{1}{2}at^{2}=\dfrac{1}{2} \cdot \dfrac{U_{2}qL^{2}}{dmv^{2}}$，其中$E_{\text{k}}=\dfrac{1}{2}mv^{2}$，解得$y_{\min}=\dfrac{1}{3}\text{cm}$，故接收屏被粒子打中的区域长度为$l=3\left( \dfrac{d}{2}-y_{\min} \right)=5\;\rm \text{cm}$