| 电表的改装 题目答案及解析
稿件来源:高途
| 电表的改装题目答案及解析如下,仅供参考!
选修3-1
第二章 恒定电流
2.4 串联电路和并联电路
电表的改装
某同学要将一满偏电流为$3\;\rm mA$的毫安表$\rm G$改装为量程为$30\;\rm mA$的电流表。他先测量出毫安表$\rm G$的电阻,然后对表进行改装,最后再利用一标准毫安表,对改装后的电流表进行检测
具体实验步骤如下:
①按电路原理图$a$连接线路
②将$R_{1}$的阻值调到最大,闭合开关$\rm S_{1}$后调节$R_{1}$的阻值,使毫安表$\rm G$的指针偏转到满刻度
③闭合$\rm S_{2}$,保持$R_{1}$不变,调节$R_{2}$的阻值,使毫安表$\rm G$的指针偏转到满刻度的三分之一的位置
④记下$R_{2}$的阻值
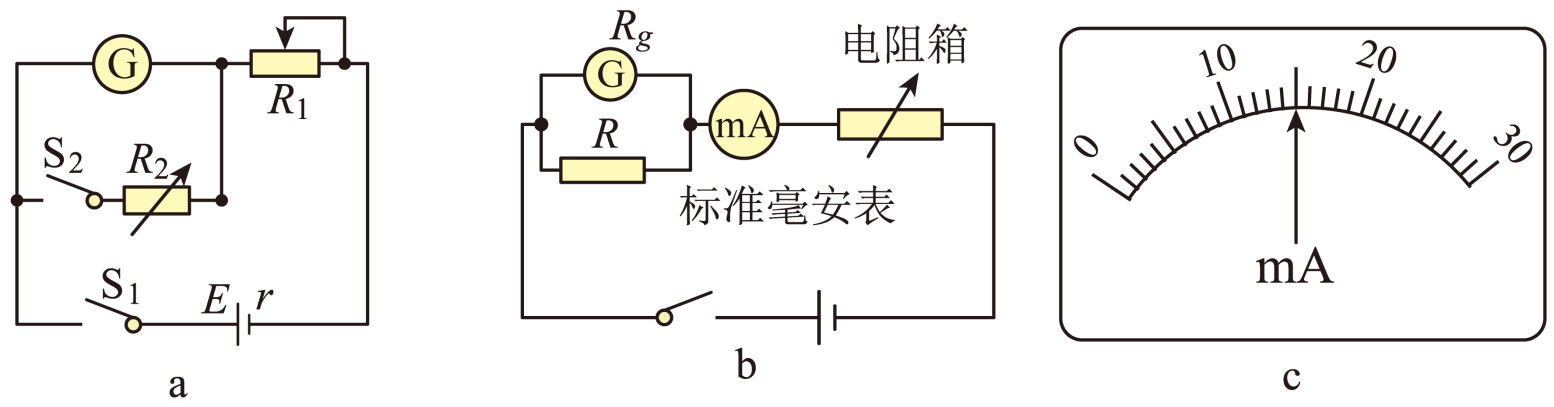
回答下列问题:
如果按正确操作步骤测得$R_{2}$的阻值为$90\;\rm \Omega$,则毫安表$\rm G$内阻的测量值$R_{g}=$ $\;\rm \Omega$,与毫安表内阻的真实值$R'_{g}$相比,$R_{g}$ $R'_{g}$(填“$\gt $”、“$=$”或“$\lt $”)
由于指针指在三分之一的位置,说明$R_{2}$分得电流为电流计电流的两倍,所以电流计电阻是$R_{2}$的两倍,为$180\;\rm \Omega$。闭合$\rm S_{2}$后,$R_{2}$与$R_{g}$的并联值$R_{并}\lt R_{g}$,所以$I_{总}\gt I_{g}$,而此时$G$的示数为满偏电流的三分之一,所以$I_{R_2}$大于三分之二满偏电流,所以$2R_{2}\lt R'_{g}$,即$Rg\lt R'_{g}$;
若忽略实验的误差,将上述毫安表$\rm G$改装成量程为$30\;\rm mA$的电流表,则需要并联一个阻值$R=$ $\;\rm \Omega$的电阻
由并联电路分流特点,得
$R=\dfrac{I_{g}R_{g}}{I-I_{g}}=\dfrac{3 \times 180}{30-3}\;\Omega=20\;\rm \Omega$
根据图$b$所示电路对改装后的电表进行检测,当标准毫安表的示数为$16.0\;\rm mA$时,改装表的指针位置如图$c$所示,由此可以推测出改装的电表量程不是预期值,改装电流表的量程是 $\;\rm mA$
标准毫安表的示数为$16.0\;\rm mA$时,改装后的电表显示为刻度盘的中值刻度,故改装电流表的量程为$32\;\rm mA$;
要达到预期目的,无论测得的内阻值是否正确,都不必重新测量,只需要将阻值为$R$的电阻换为一个阻值为$kR$的电阻即可,其中$k=$ 。
把毫安表改装成电流表需要并联分流电阻,并联电阻阻值$R=\dfrac{I_{g}R_{g}}{I-I_{g}}$
当量程为$32\;\rm mA$时,则有$R=\dfrac{3 \times 10^{- 3}R_{g}}{(32-3) \times 10^{- 3}}=\dfrac{3R_{g}}{29}$
当量程为$30\;\rm mA$时,则有$kR=\dfrac{3 \times 10^{- 3}R_{g}}{(30-3) \times 10^{- 3}}=\dfrac{3R_{g}}{27}$
联立解得$k=\dfrac{29}{27}$
| 电表的改装题目答案及解析(完整版)
