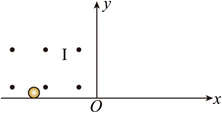
$O$点时的速度大小；

$\\dfrac{mg}{qB}$

小球到$O$点时恰好对水平而无压力，应有$mg=qvB$

得$v=\dfrac{mg}{qB}$

求匀强电场的场强的大小；

$\\dfrac{mg}{q}$

由题意$mg=qE$

即$E=\dfrac{mg}{q}$

若磁场Ⅱ为圆形，求该磁场最小面积；

$\\dfrac{\\pi m^{4}g^{2}}{16q^{4}B^{4}}$

如图

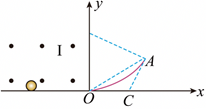
若磁场Ⅱ为圆形，根据几何关系可知，线段$OA=R$，根据$2qvB=m\dfrac{v^{2}}{R}$

所以$R=\dfrac{m^{2}g}{2q^{2}B^{2}}$

圆形磁场的半径为$\dfrac{1}{2}R$。该磁场最小面积$S_{1}=\pi\left(\dfrac{1}{2}R\right)^{2}=\dfrac{\pi m^{4}g^{2}}{16q^{4}B^{4}}$

若磁场Ⅱ为矩形，求该磁场最小面积；

$\\dfrac{(2-\\sqrt{3})m^{4}g^{2}}{8q^{4}B^{4}}$

若磁场Ⅱ为矩形，根据几何当系可矨，该矩形长为$R$，宽为$R(1-\cos30^\circ)$。该磁场最小面积$S_{2}=R\cdot R(1-\cos30^\circ)= \dfrac{(2-\sqrt{3})m^{4}g^{2}}{8q^{4}B^{4}}$

若磁场Ⅱ为三角形，三角形三个顶点为$O$、$A$、$C$（$A$、$C$两点图中均未画出），当该磁场面积最小时，求$A$、$C$两点的坐标。

$A$的坐标为$\\left(\\dfrac{\\sqrt{3}m^{2}g}{4q^{2}B^{2}},\\dfrac{m^{2}g}{4q^{2}B^{2}}\\right)$，$C$的坐标为$\\left(\\dfrac{\\sqrt{3}m^{2}g}{6q^{2}B^{2}},0\\right)$

小球在磁场Ⅱ区域运动的轨迹如图，$\Delta OAC$要完全覆盖圆弧$\overparen{OA}$，因此$OC$和$AC$必须与圆弧$\overparen{OA}$相切，由于线段$OA=R$。

$A$的坐标为$\left(\dfrac{\sqrt{3}m^{2}g}{4q^{2}B^{2}},\dfrac{m^{2}g}{4q^{2}B^{2}}\right)$，$C$的坐标为$\left(\dfrac{\sqrt{3}m^{2}g}{6q^{2}B^{2}},0\right)$