实验小组用图甲所示装置研究电子在平行金属板间的运动。将放射源$P$靠近速度选择器，速度选择器中磁感应强度为$B$（垂直纸面向里），电场强度为$E$（竖直向下）、$P$能沿水平方向发出不同速率的电子。某速率粒子能沿直线通过速度选择器，再沿平行金属板$A$、$B$的中轴线$O_{1}O_{2}$射出板间。已知水平金属板长为$L$、间距为$d$，两板间加有图乙所示的交变电压，电子的电荷量为$e$，质量为$m$（电子重力及相互间作用力忽略不计），以下说法中正确的有$(\qquad)$

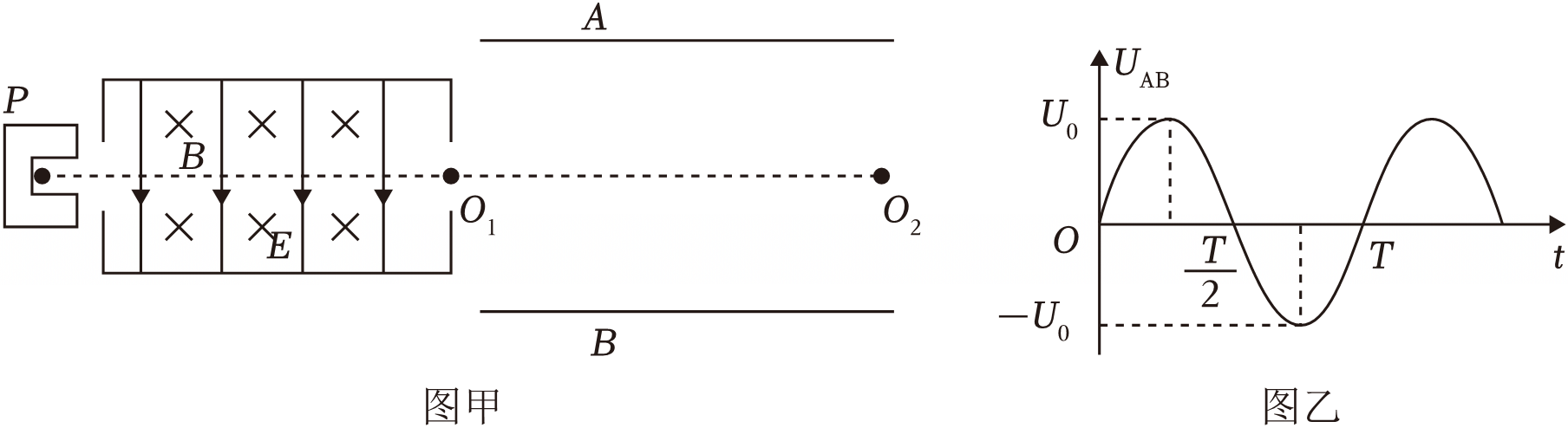
沿直线穿过速度选择器的电子的速率为$\\dfrac{E}{B}$

只增大速度选择器中的电场强度$E$，沿中轴线射入的电子穿过板间的时间变长

若$t=\\dfrac{T}{4}$时刻进入$A$、$B$板间的电子恰能水平飞出金属板的位置一定在$O_{2}$点

若$t=0$时刻进入金属板间$A$、$B$的电子恰能水平飞出，则$T=\\dfrac{BL}{nE}(n=1,2,3…)$

$\rm A$、沿直线穿过速度选择器的电子所受洛伦兹力与电场力平衡，即$evB=eE$

解得电子的速率为：$v=\dfrac{E}{B}$，故$\rm A$正确；

$\rm B$、只增大速度选择器中的电场强度$E$，根据$\rm A$选项的结论：$v=\dfrac{E}{B}$，可知沿中轴线射入金属板$A$、$B$间的电子速率增大，电子沿中轴线的方向做匀速直线运动，由$t= \dfrac{L}{v}$可知穿过板间的时间变短，故$\rm B$错误；

$\rm C$、若$t=\dfrac{T}{4}$时刻进入$A$、$B$板间的电子始终在板间运动，其运动过程如下：

$\dfrac{T}{4}\sim \dfrac{T}{2}$时间内，电子在竖直方向向上加速运动，$\dfrac{T}{2}\sim \dfrac{3T}{4}$时间内，电子在竖直方向向上减速运动，在$\dfrac{3T}{4}$时刻竖直方向的速度为零，位置在中轴线上方；$\dfrac{3T}{4}\sim T$时间内，电子沿竖直方向向下加速运动，$T\sim \dfrac{5T}{4}$时间内，电子在竖直方向向下减速运动，在$\dfrac{5T}{4}$时刻竖直方向的速度为零，位置恰好在中轴线上，之后电子如此反复周期性运动且运动周期为$T$。

由上述分析可知，电子在$\dfrac{3T}{4} +nT(n=0,1,2,3…)$时刻速度为水平方向，若此刻飞出电场，其位置在$O_{2}$点上方；

电子在$\dfrac{5T}{4} +nT(n=0,1,2,3…)$时刻速度为水平方向，若此刻飞出电场，其位置在$O_{2}$点，故$\rm C$错误；

$\rm D$、若$t=0$时刻进入金属板间$A$、$B$的电子恰能水平飞出，与$\rm C$选项同理，电子射出金属板的时刻为：$t=nT(n=0,1,2,3…)$

则电子的速率为：$v=\dfrac{L}{t}=\dfrac{L}{nT}(n=1,2,3…)$

与$\rm A$选项的结果$v=\dfrac{E}{B}$，联立可得：$T=\dfrac{BL}{nE}(n=1,2,3…)$，故$\rm D$正确。

故选：$\rm AD$。